信用风险是金融创新的其本质，经营金融创新就是经营信用风险。我国资本消费市场有40万亿元的优先股、80万亿元规模的国债，股权投资人囊括金融机构、基金公司、保险业务、基金及中小散户。专精政府机构股权投资人所持了大量的优先股、国债及期货市场、套期保值等其他衍生产品，分担了巨大信用风险，怎样管理工作信用风险是每家政府机构股权投资人不得已直面的问题。在险商业价值（Value at Risk），全称VaR微积分模型，蓬勃发展于上世纪90年代，JP Morgan将其弘扬，创办了RiskMetrics系统。目前VaR微积分模型已被广泛运用于各金融创新政府机构的消费市场信用风险计算方法和管理工作。
VaR是指在某一机率密度表达式下股权投资女团在未来某几天的最小可能将经济损失，从微积分上看它来衡量的是股权投资女团当期原产的分四位数，假定 cc是他们选择的机率密度表达式，则VaR相关联于当期原产的1−c1-c 下尾处。例如机率密度表达式为95%，则VaR等同于当期原产表达式的5%行政处分四位数。
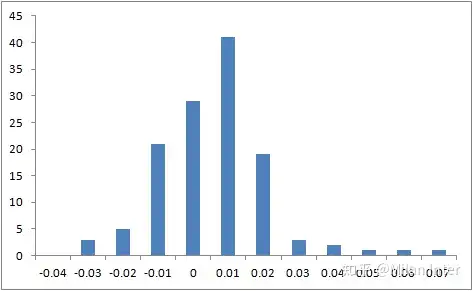
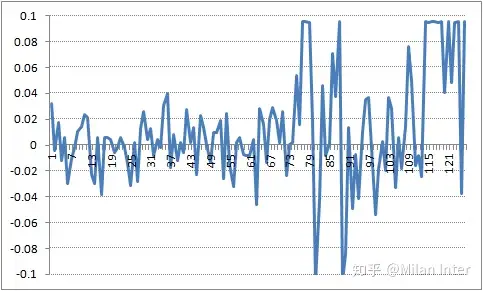
先譬如说怎样排序一般而言优先股的VaR值，他们以上市公司国海证券为例，假定当前我所持100万总市值的西南证券优先股，那么今晚我的股权投资女团最小净亏损可能将是多少？从图1可以窥见，国海证券在2019年三季度总共126个季度的日利率发生变动区段在基本在-6%与6%之间，其利率原产的柱形图如图2所示，他们去从小到大排序的第5%、约莫在6/126的位置，得出结论该分四位数的值为-2.35%，即今天100万总市值的国海证券今晚95%的机率下最小净亏损2.35万。该2.35万即为95%机率密度表达式下的一天VaR值。
后面排序VaR的方式是透过优先股发展史利率数据求出科杨桐四位数，称作发展史lussin。另一种排序VaR值得称赞方式为模块法（也称微积分模型法），该方式不直接透过发展史利率求出分四位数，而是需要假定利率的机率原产表达式，从而透过利率的机率密度表达式求出相关联机率密度表达式的分残基。他们仍然以优先股国海证券为例，如果他们假定国海证券日利率的原产表达式为均值0的正态原产，其标准差σ\sigma 可以透过发展史数据求出结果为1.60%，而标准正态原产的5%分残基的随机变量值为1.645，因此在正态原产假定下95%机率密度表达式下的一天VaR值为 1.645×0.0161.645 \times 0.016 ,即2.64%，约大于发展史lussin的结果2.35%。相应的， nn 天的VaR值为 1.645∗n∗σ1.645*\sqrt{n}*\sigma 。
在实际的信用风险管理工作过程中，总规模限制是最常见的信用风险控制指标，限制总规模一定程度上限制了女团的最小净亏损，但无法来衡量经济损失的机率问题。例如同样的100万总市值的两个股权投资女团，女团A所持100万总市值的国海证券优先股，女团B所持100万总市值的星期六优先股，星期六的当期原产图如图3所示。将图3和图1相比较，很明显星期六的波动幅度大于国海证券，事实上，在同样的正态原产假定下，星期六的利率标准差为4.10%，是国海证券波动的两倍有余，其VaR值为6.73%，因此，从VaR角度看，所持优先股星期六的信用风险远远大于所持同样总市值的国海证券，所持国海证券我有95%的机率最小净亏损不超过2.64%，而所持星期六我只能保证95%的机率最小经济损失不超过6.73%。
同样的逻辑也适合国债股权投资女团，他们常用久期、凸性、基点商业价值等指标来衡量国债对利率发生变动的敏感性，例如某国债股权投资女团的基点商业价值为100万元，则在利率上升100bp的情况下，该女团将净亏损1亿元。如果进一步引入该女团的VaR值，则可以回答该股权投资女团在某机率下的最小净亏损，因为利率发生变动存在某机率原产。总之，VaR将敞口类指标与机率统计相结合，给出了女团潜在经济损失的机率边界，可以更加直观的理解股权投资女团的可能将经济损失情况。
在实际的信用风险管理工作操作中，VaR天数的选择较为主观，但也不是随意的，像优先股、场内衍生产品等资产可以排序一天期限的VaR值，因为该类资产流动性高，在一定规模下可以快速变现；但是银行间国债（特别是cp、scp、ppn等）流动性极差，一天内全部卖出及其困难，因此实务中可以选择较长期限的VaR值，如10天或者1个月。
VaR来衡量的是消费市场正常波动下的尾部经济损失，即消费市场正常波动下的极端经济损失，它解释的是消费市场正常波动下的最小可能将经济损失，而不是消费市场极端情形下的经济损失。而算得上极端情形的应该是战争、政治、金融创新危机等重大发生变动。因此，VaR并没有度量最坏情况下的损失，需要采取其他方式进行补充，如压力测试技术，压力测试可以人为设置极端最坏情景，是VaR微积分模型的不可或缺的度量极端信用风险的补充指标。知乎上有人将VaR微积分模型视为史上最蠢的指标(见https://www.zhihu.com/question/21774616/answer/19739484），在此我不敢苟同，在我看来这是因为大家对VaR的期望太高，很多人对VaR不满意的地方主要在于两点，一是建模准确性问题，发展史lussin排序VaR太过依赖尾部数据，模块法下的正态原产假定不准确，因为几乎不存在刚好符合正态原产的金融创新时间序列，且大部分序列都是厚尾的，因此低估了尾部信用风险，这些的确都是VaR微积分模型的缺点，但是大家都知道，所有建模都是错误的，但是有些微积分模型是有用的，建模就是离不开假定。VaR微积分模型普遍作为一种消费市场信用风险度量指标，和金融创新衍生产品定价不同，其精确度的不足完全可以忍受，而衍生产品定价则对准确度要求要高许多，却在风险中性定价原理中（如Black-Scholes套期保值定价微积分模型），同样作了正态原产的假定。对VaR微积分模型的第二点不满意的地方在于其对极端经济损失的度量不足，这就是典型的期望过高，因为VaR度量的是消费市场正常波动下的极端经济损失，VaR只是一把杀猪刀，不是屠龙刀，但是没人说杀猪刀最蠢最没用，因为杀猪刀本来就只能杀猪，不能屠龙，你想让杀猪刀有屠龙刀的功能，就只能说杀猪刀没用了。杀猪刀的升级版就是压力测试，以及预期经济损失微积分模型（ES微积分模型），ES微积分模型度量的是女团超过VaR值的平均经济损失，的确更能反映尾部信用风险，但是它不易于理解，ES微积分模型度量的是尾部平均经济损失，但是其波动范围多大？微积分模型没有提供解释，另一方面，ES微积分模型无法验证其有效性，因此总的说来在实用性上ES微积分模型并不如VaR微积分模型。而未来真的会有人研究出屠龙刀吗？恐怕很难，在金融创新危机等极端情形下，整个金融创新系统的系统性信用风险很容易将自己击溃，而这种极端事件的发生可能将性微乎其微，所以他们在日常经营中无需时常采取准备措施预防这种系统性信用风险，不然只会造成资本资源的浪费。因此，不管是VaR微积分模型，还是其他信用风险计算方法指标，都只是信用风险管理工作的一方面，它们始终代替不了经验、判断，在面临可能将到来的系统性信用风险等极端情形时，经验和判断可以让他们提前消除信用风险，这才是最有效的信用风险管理工作。
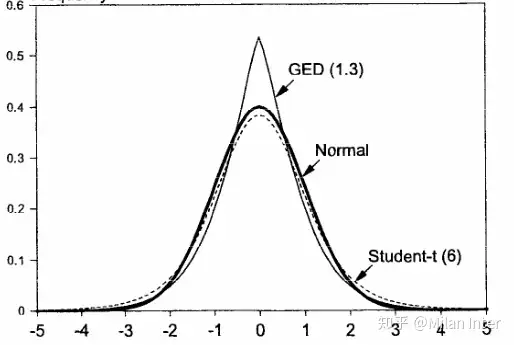
正态原产由于其排序的方便性已经被广泛应用于金融创新时间序列分析，虽然它不是拟合金融创新时间序列的最佳原产。金融创新时间序列常表现出尖峰厚尾性，因此实务中也会对金融创新序列做其他原产假定，最常用的有t原产以及广义误差原产（GED原产）。t原产的原产表达式有一个自由度模块nn ， nn 越小则原产的厚尾性越好，而当 nn越大时，t原产就趋近于正态原产。广义误差原产与t原产类似，也能更好的拟合尖峰厚尾特征，正态原产就是广义误差原产的一种特殊情况。
