面试必问系列—深浅拷贝✔️ - 网站源码_资源分享

正逢大学毕业季，绝大部分人能碰到迈向社会风气的第二个痛点—找组织工作复试，当你历经的复试多了，就会辨认出会有许多复试官时常问及的难题，比如说：

问：你为何会优先选择他们子公司？

答：我子公司并非圣索弗勒维孔特嘛

所以，就要在那个系列产品里谈谈这些时常被问及的复试题

那时先让他们一起来介绍呵呵厚薄复本

表达式

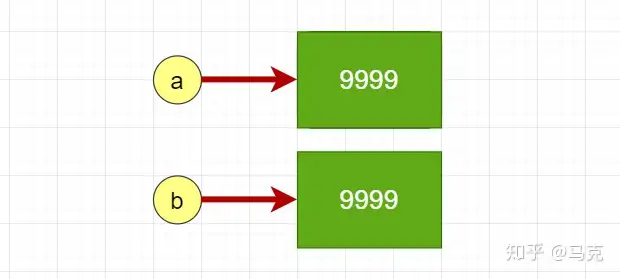
在Python中，表达式只不过是第一类的提及。

a = 9999 b = a print(a) #ouput:9999 print(b) #ouput:9999 print(id(a)) #ouput:1869259054928 print(id(b)) #ouput:1869259054928

这种表达式后，b和a不但在值上成正比，所以是同一第一类，换句话说在堆缓存中只有一个数据第一类9999，这两个变量都指向这一个数据第一类。从数据第一类的角度上看，那个数据第一类有两个提及，只有这两个提及都没了的时候，堆缓存中的数据第一类9999才会等待垃圾回收器回收。

需要注意的是，它和下面的表达式过程是不等价的：

a = 9999 b = 9999 print(id(a)) #ouput:1869266158672 print(id(b)) #ouput:1869266158768

虽然a和b的值成正比，但他们并非同一第一类，这时候在堆缓存中有两个数据第一类，只不过这两个数据第一类的值成正比。

不可变第一类

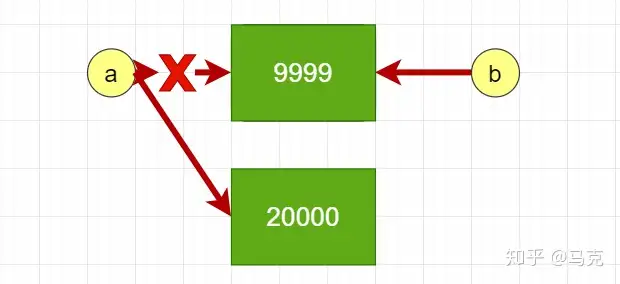
对于不可变第一类，修改变量的值意味着在缓存中要新创建一个数据第一类

>>> a = 9999 >>> b = a >>> id(a) 2625562451792 >>> id(b) 2625562451792 >>> a = 20000 >>> id(a) 2625564836944 >>> id(b) 2625562451792

在a重新表达式之前，b和a都指向堆缓存中的同一数据第一类9999，但a重新表达式后，因为数值类型9999是不可变第一类，不能在原始缓存块中直接修改数据，所以会新创建一个数据第一类保存20000，最后a将指向那个20000第一类。这时候b仍然指向9999，而a则指向20000。

可变第一类

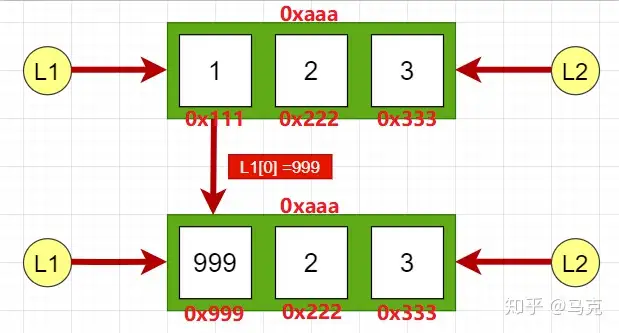
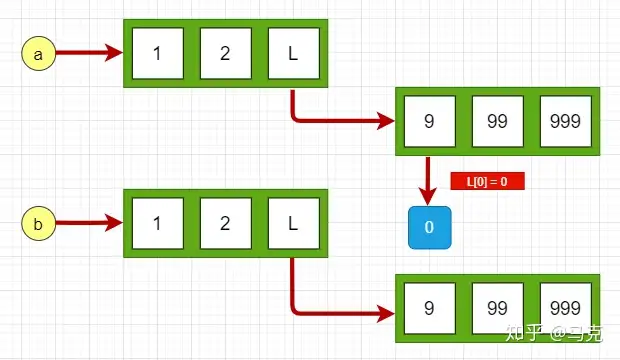
对于可变第一类，比如说列表，它是在”原处修改”数据第一类的。比如说修改列表中的某个元素，列表的地址不会变，还是原来的那个缓存第一类，所以称之为”原处修改”。例如：

>>> L1 = [1,2,3] >>> L2 = L1 >>> L1[0] = 999 >>> L1,L2 ([999, 2, 3], [999, 2, 3]) >>> id(L1) 2625562620872 >>> id(L2) 2625562620872

在L1[0]表达式的前后，数据第一类[1,2,3]的地址一直都没有改变，但是那个列表的第二个元素的值已经改变了。因为L1和L2都指向那个列表，所以L1修改第二个元素后，L2的值也相应地到影响。也就是说，L1和L2仍然是同一列表第一类。

PS:

为啥一直在用9999那个数？

答：1. 9是我的幸运数字:joy:

2. 因为9999并非小整数（移步文章末尾）

为何在Pycharm内的输出结果和上面内容不一致？

答：首先 Python给[-5,256]以内值分配了空间，超出的就需要重新分配。而Pycharm不遵循那个，因为 Pycharm是放到脚本里面编译的，而并非在解释器里面，脚本编译是一次性编译的会产生编译文件，所以缓存地址会复用，所以输出的id效果不一致。

浅复本

浅复本：只复本第一层的数据。

在python中表达式操作或copy模块的copy()是浅复本

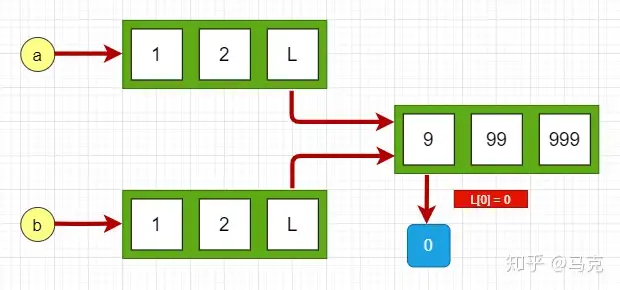
怎么理解复本第一层的数据，先来看一个嵌套的数据结构：

L1 = [1,2,3] L2 = [1,2,[3,33,333]]

L1只有一层深度，L2有两层深度，浅复本时只复本第一层的数据作为副本，深复本递归复本所有层次的数据作为副本。

例如：

>>> import copy >>> L = [9,99,999] >>> a = [1,2,L] >>> b = copy.copy(a) >>> a,b ([1, 2, [9, 99, 999]], [1, 2, [9, 99, 999]]) >>> id(a),id(b) # 不成正比 (2625565288456, 2625565288776) >>> id(a[2]) 2625565288328 >>> id(b[2]) # 成正比 2625565288328 >>> L[0] = 0 >>> a,b ([1, 2, [0, 99, 999]], [1, 2, [0, 99, 999]])

a 和 b 是一个独立的第一类，但他们的子第一类还是指向统一第一类（是提及）。

深复本

深复本：递归复本所有层次的数据

Python中copy模块的deepcopy()是深复本 ,比如说：

>>> L = [9,99,999] >>> a = [1,2,L] >>> b = copy.deepcopy(a) >>> a,b ([1, 2, [9, 99, 999]], [1, 2, [9, 99, 999]]) >>> id(a),id(b) # 不成正比 (2625565169224, 2625565169288) >>> id(a[2]) 2625565169480 >>> id(b[2]) # 不成正比 2625565169416 >>> L[0] = 0 >>> a,b ([1, 2, [0, 99, 999]], [1, 2, [9, 99, 999]])

深度复本, a 和 b 完全复本了父第一类及其子第一类，两者是完全独立的。

一般来说，浅复本或者提及表达式是他们所时常用的操作，只有少数情况下( 数据序列化、要传输、要持久化 )，才需要深复本操作，但是这些操作一般都内置在对应函数中，无需手动去深复本。

总结：

浅复本：缓存地址深复本：数据内容

早已存在的小整数

数值第一类是不可变第一类，理论上每个数值都会创建新第一类。

但实际上并并非这种，对于 [-5,256]那个区间内的小整数，因为Python内部提及过多，这些整数在python运行的时候就事先创建好并编译好第一类了。所以，a=2, b=2, c=2根本不会在缓存中新创建数据第一类2，而是提及早已创建好的初始化数值2。

>>> a=2 >>> b=2 >>> a is b True

对于超出小整数范围的数值，每一次使用数值第一类都创建一个新数据第一类。例如:

>>> a=9999 >>> b=9999 >>> a is b False

但是也有特殊的情况：

>>> a=9999;b=9999 >>> a is b True >>> a,b=9999,9999 >>> a is b True

为何会这种呢？

原因是 Python解析代码的方式是按行解释的，读一行解释一行，创建了第二个9999时辨认出本行后面还要使用一个9999，于是b也会使用那个9999，所以它返回True。而前面的换行表达式的方式，在解释完一行后就会立即忘记之前已经创建过9999的数据第一类，于是会为b创建另一个9999，所以它返回False。

如果在Python的文件中执行，则在同一作用域内，a is b是一直会是True的，这和代码块作用域有关：整个py文件是一个模块作用域，可以看我之前的内容