答案定位:
既不是儿童级别的读物,也不涉及高深晦涩和非常专业的词句。该答案的目的是让有初中文凭的人读懂。前言:
你需要有一定的电学知识,然后就可以去看模拟电路和数字电路相关的书籍了,了解完这两个东西后你就能基本明白计算机是怎么运作起来的了。这里只做简单回答。简单回答的意思是说,这个回答旨在让完全没有基础的人从理念上了解计算机如何运作—-针对这一原则,答主会一切围绕通俗易懂来展开,因此在某些学术细节上或许有错。读懂此答案需要具备的能力:
初中电学和数学知识 + 二进制的基本知识。对于掌握了初中数学知识的朋友来说,大致了解二进制是很简单的,在这里做个简单介绍:
我们知道十进制是最常见的数制,它有十个数字0-9。二进制也同理,只不过二进制是两个数字。因此十进制里的“逢十进一”在二进制中变成了“逢二进一”。
十进制数数:1 2 3 4 5 6 7 8 9 10 11 12 …
二进制数数:1 10 11 100 101 110 111 1000 1001 …
正文:
1)半导体的发现。人类有一天被上帝丢下来的硅不小心砸到了脑袋,于是乎发现了半导体。用半导体材料可以制成二极管。
二极管的原理:给半导体材料里掺入某种元素后,半导体会这样:我讨厌电子;而给半导体掺入另外一种元素后,半导体会这样:我喜欢电子。我们把一个讨厌电子的半导体和一个喜欢电子的半导体放在一起的时候,在它们之间就会形成一个电子趋向的力量(半导体毕竟不是导体,半导体的原子核对电子的束缚力是足够大的,因此虽然有趋向,但不足以让一侧的电子跑到另一侧 — 这也就是为什么它叫做“半导体”),这就是一个二极管了。当二极管外部有电流通过的时候,如果外部电流内的电子的运动方向顺从了其内部的这种电子的趋向,则这个二极管可以视为接通的导线;而如果外部电流的电子运动方向和二极管内部的电子方向相反的时候,外部电流就无法通过这个二极管(除非加了很高的反向电压 —– 这样就会将二极管击穿 —- 当然我们在使用二极管时不会让它被击穿因此这里无需考虑这种情况),此时这个二极管可以视为断路。所以在二极管的电路里,根据二极管两端的电压的高低的不同,就能测出某些电阻两端的电压有不同的数值:高或者低(具体看下面的4)。
2)数学上有二进制:0和1。由于只有两个数字,因此恰好可以和上面的高低电压一一对应起来。比如我们可以规定:1表示高电压0表示低电压。
3)就像四则运算中的加减乘除一样,对于二进制我们有配套的逻辑运算:与、或、非。
与:
0与0=0
1与0=0
0与1=0
1与1=1
一句话描述:“只要有0结果就是0”。
或:
0或0=0
1或0=1
0或1=1
1或1=1
一句话描述:“只要有1结果就是1”。
非:
非0=1
非1=0
还有其他逻辑运算比如同或、异或等就不一一列举了;总之基础的逻辑运算就这三个。
4)把123联系起来,人类做出了:与门电路、或门电路、非门电路、异或电路等。
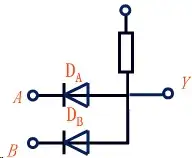
注:
上图中最上面的唯一一个没有被字母标记的结点在这里记为:C
A、B和C都可以加上一定的电压;Y为测量端;DA与DB为二极管;C下面的矩形为电阻。
这是一个与门电路,有初中电学知识就应该可以看懂。大概很简单地解释下(其实不太对但是不影响你从原理上理解):
当A和B中任意一端是0V(可以理解为接地)而C端有一定的电压时(中学生理解方式:用导线将AB两点连接在一起后再连接到直流电源的负极,C点接正极),测量Y端电压(Y与大地间的电压或者说Y与0间的电压)几乎是0V。这是因为AB中至少有一个是0V且二极管的方向是那个样子的,所以电流从C端流入、通过那个电阻后从0V那里流入大地/回到负极了,因此此时测量Y端电压等于在测量一个导通的电路中的一段导线上的电压,所以很显然几乎是0V。而如果AB端电压都比较高(高于C端的电压但是没有到击穿的地步)的时候(中学生理解方式:用导线将AB两点连接在一起后再连接到直流电源的正极,C点接负极),两个二极管都等效于断路状态,电流试图从AB端流向右边(因为AB端电压高于C端电压因此电流的趋向是从AB流向C)但是流不过去,所以此时测量Y端电压的时候就不是0V了而是有一定的数值。
因此,在这个电路中,只有当AB两端同时有高电压时,Y端才有电压(大于0V);AB中只要有一个是0V,Y端就是0V。当我们把AB两端视为输入Y端视为输出时,(用一个黑盒子把整个电路装起来让你看不到,你只能看到从这个黑盒子里伸出来的三个接头:A,B和Y)
就可以得到和上面的“与运算”相对应的结果(设高电压=1 低电压=0):只有输入都是1的时候输出才是1,其他时候都是0。这就是一个与门电路。同理,也有类似的或门电路等等。
5)有了这些门,就可以做半加器了,有了半加器就能做全加器,它的作用是实现加法。同理,可以实现四则运算了(如何用这些门实现四则运算,这里不细说,否则就违背了“通俗易懂”的原则。但这样的跨度有点大,因此后面的BONUS里有介绍这部分内容)。到了这里,理论上只要我给你相关的材料,你就可以做出一个有一定功能的电路了。比如你可以做一个:输入三个数字,把前两个数字相加的结果乘以第三个数字然后输出结果。
比如,你输入“高低低高”给一个电路,然后这个电路给你输出“高低高低”。如果我们之前已经规定了高电压表示1、低电压表示0,即:1001为输入,1010为输出,显然,这就是做了一个加1的运算。
当然,由于你电路里的所有门电路都是盯死在线路板上的,所以你的这个电路永远只能做这一件事。然后你就可以做一个专门卖这种功能电路板的硬件生产商了。像计算机里的那些固定在硬件上的指令,就是这么来的。所谓硬件上的那些指令,就是:你输入某些数字,硬件就做相关运算,然后输出结果。
很多朋友会在这里产生一个困惑(这个困惑甚至困扰着很多计算机专业的学生):你说用1表示高电压0表示低电压,那我怎么告诉电路这里是高电压或者低电压、电路又是怎么告诉我那里是高电压或者低电压呢?
本质上,这个问题是在问:电路和人如何交流,或者说是在问电路的输入输出设备是什么。
到目前为止,我们所需要用到的输入输出设备其实非常简单:输入设备就是一个个的开关 — 开关接通则给电路输入高电压开关断开则给电路输入低电压;输出设备则是一个个的发光二极管或者简单理解为“灯泡” — “灯泡”亮则表示电路输出了高电压“灯泡”不亮则表示电路输出了低电压。有了这样的输入输出设备,你就可以这样做了:通过控制一系列开关的状态,给电路输入高电压和低电压(即0和1);而后通过观察一系列“灯泡”的状态,来得到电路输出的结果。
6)逻辑完备性。这个世界中的万事万物都可以用三种顺序来表示出来:顺序、选择和循环。完备的意思就是说某个理论系统可以涵盖所有的情况,没有例外。
注:以下两个斜杠后面的部分属于注释,负责解释说明本行做了什么。
顺序:从第一行到第二行再从第二行到第三行……(就像你看文章一样,一行一行地看)
选择:如果某个条件满足(比如x<y)就到第p行;如果不满足(比如x>=y)就到第q行
循环:如果某个条件不满足/满足(比如a<x)就到第p行,什么时候该条件满足/不满足了(比如a>=x)了就到第q行
用这三个可以表示世间万物。
比如:你上楼梯回家:
a—打开楼门,面前出现一个10个台阶的楼梯
b—循环做登楼梯的动作直到做了10次
c—如果面对的是你家,开门,到e;如果不是,向右转
d—如果到家了,到e;否则,到c
e—结束
7)图灵机。图灵机简单来说就是一个能接受信息、处理信息和发出信息的虚构的机器。世间万物皆为图灵机。
比如,一个杯子放在一张桌子上:
输入:杯子
图灵机:桌子
输出:支持杯子或者说杯子没有掉下去
输入:谢谢
图灵机:你
输出:不客气
再比如6中的那个回家的例子:
输入:十个台阶的楼梯
图灵机:你
输出:重复十次登楼梯动作
当然,你这个图灵机在对信息的处理上远远比一张桌子要复杂得多:
如果 (十个台阶上面是你家 而且 你面对着台阶)
那么 (循环十次登楼梯动作)
当然,你不会是如此简单的一个图灵机。你还会这样:
在登楼梯过程中,如果有人通过你的耳朵给你输入:儿子别回家了,咱们到外面吃饭。
你这个图灵机就会立刻优先对这个新的输入进行处理而会将登楼梯的动作挂起(挂起的意思就是暂时不执行)
你会这样:
如果(声音是你爸或者你妈的)
那么(转身下楼梯)
否则 // 就是说声音不是你爸也不是你妈的
那么(唤醒刚才挂起的登楼梯的动作继续做)回到家后,你这个图灵机会从你大脑里调出晚上要做的事情:写作业、看电视、睡觉
然后你会给这些任务排列一个优先级:比如写作业是1,看电视是2,睡觉是3。(坏孩子的任务优先序列可能是:看电视1,写作业2,睡觉3---小朋友们不要学哟)
你会根据哪个优先级更高来选择先做哪一个。
当然,远没有这么简单。比如:
如果(你正在做1 而且 时间已经12点了)
那么 (你决定停止1,直接做3,同时准备好明天给你们老师的输出 — 跟他解释你为什么没写完作业)
……
……
……
所以人是一个非常非常非常非常复杂的图灵机。由于现在的5那里的硬件落后得和渣一样,所以人类目前根本无法用电路去模拟一个真人 。即使硬件发达到可以模拟真人了,那么依然也只是模拟。人类最大的本领:学习,只靠发达的硬件还是无法做到。所以人类到底能不能真的用电路去实现一个真正的人类的大脑,这是一个悬而未决的问题,有的人认为可以,有的认为不可以。
6+7:这个宇宙中的一切,都可以抽象成图灵机;这个世界上的所有事件,都可以用那三种逻辑来表示。 而用上面的5中的内容,可以在电路上实现6+7。只要电路的速度越来越快,我们就能实现越来越复杂的6+7。 图灵机,只是一个概念上的虚拟的机器。而人类可以通过各种手段去实现各式各样的图灵机:人类制造的机器,是图灵机;人类盖的楼房,是图灵机;哪怕人类生了一个婴儿,那个婴儿也是一个图灵机。计算机,只是众多图灵机中的一种。只要一个图灵机具备了6中所说的三种顺序的逻辑能力,那么这个图灵机理论上来说就可以模拟宇宙万物了。
比如在5)那里的那个做加1运算的“东西”—–其实那就是一台计算机。只不过它的输入是一个个的开关,而不是键盘和鼠标;它的输出是一个发光二极管闪了几下,而不是显示器和打印机。一个遥控器、一个手机、一个红白机,都是计算机、都是图灵机。
8)在半导体的基础上,如果加入一些其他化学元素(具体请去看模拟电路的书),就可以让半导体的状态变得“可擦除”和“可记忆”:比如上次这里是断路半导体状态、现在我可以改成连通的。我给一个电路板接通电路,然后给它某些输入、改变了里面的某些半导体的状态,然后断开电路,由于这种半导体是可记忆的,所以它里面的每个门电路都是你断电之前的状态,下次再接上电源的时候,就能读出上次的状态---这样就可以存储数据了。
9)振荡器。高中物理会学振荡回路。就是电磁一直相互转化而形成振荡,就和广播的道理一样。振荡的频率是固定的,比如每秒震荡100次,每振荡一次,就发射出一个电压信号。然后cpu每接收到一次电压信号,就去读一条指令(看6,类似这样:如果收到了电压信号,则执行***。当然还要有外来的用户输入,比如如果用户输入了1,同时接收到了电压信号,则执行a;如果没有用户输入,则执行b;如果用户第一次输入0第二次输入1,则执行c……)—–指令就是根据5那里被硬件生产商固定在硬件里的半导体的通断状态。一般你买电脑的时候都有个内存频率,单位都是MHz,表示一秒钟这个内存里的振荡器可以发送多少百万次信号。
到了这里,你就可以做出一个能处理四则运算和拉丁字母(拉丁字母可以和数字一一对应起来)的电路板了。
10)卷积定理+(离散)傅立叶变换+采样。大学数学基础课会学傅立叶变换,数学专业的某个方向会学卷积定理。你不需要知道它们是什么东西,你只需要这三个东西合起来能做这样一件事:
真实世界的信息转换成连续信号、连续信号转换成数字信号。
虽然我们永远不能把真实世界的信息零误差地转换为数字信号,但是可以无限逼近。由于人类太弱了感官系统太不敏感了,所以只要差不多逼近一点人是根本察觉不出来的。世界上有无数种红色,但计算机只要提供256种红色,人就以为能表示所有的红色了。
自此,你就可以做一个能处理数字、文字、声音和图像的机器了。简单来说,只要能被转化成数字的信号,就都可以被计算机处理。
比如我们要处理256种颜色,那么我们只要把这些数字和1-256这些数字一一对应起来,那么当计算机要处理第一种颜色时,它只需要对数字1进行处理即可;当计算机处理完毕后,我们再把处理后的数字转换回它对应的颜色即可。这个过程就像是电话的原理:声波转换成电磁信号电磁信号最后又转换回声波。
11)荧光物质可以在受到不同能量的电子的轰击下发出不同的颜色,根据三原色原理,我们可以通过对电子加压的控制达到显示不同颜色的目的———————显示器。
12)键盘底下有一张导电的纸,你按下某个键,就等于接通了某些电路,就有一个独一无二的输出,你只要事先规定好哪种输出对应哪个键,主机就能够知道你按下了某个键了。比如规定“高低高高低低高高低”是K,那么主机只要从键盘那里接收到了101100110就知道用户按下了K。
鼠标:鼠标下面的光源发射器会向桌子发光,还有个光的接收器。当你移动鼠标时,接收器可以感知到发射器发出的光反射回来时的入射角和方向的不同变化,然后就可以以不同电信号的方式告诉主机鼠标在向着那个方向移动;鼠标点击的原理和键盘类似,不再赘述。把制作上面所有物件的材料都买齐了,然后你就能自己攒一个计算机出来了………….Good luck!
====================================================================
上面说的这些其实非常粗浅,想知道完备的系统的知识请在上大学时报考计算机或通信专业: 通信就是把信息从自然界里捕捉到然后再转化成易处理的信息然后再通过各种方法传输最后到了信息处理的终端:计算机 这里。计算机处理信息后再把信息通过各种各样的方式传递出来。=========================== BONUS ==========================
关于6:逻辑完备性。
如上所述,逻辑的完备性靠三种逻辑顺序实现:顺序、选择和循环。
用这三种逻辑顺序可以解决问题,比如上面7中的“回家”。这里再举一例:
计算从1到100的所有奇数的和。
上面这个例子中把三种逻辑顺序已经都涉及到了。
依照这三种逻辑来描述世间的一切问题,可以把问题分为三类:
1)不可解决的问题。
虽然前面说了,用这三种逻辑顺序可以表示一切事物但是这并不意味着可以解决一切问题。
举个例子:
显示自己本身的所有代码。
什么意思呢?就是说你写一段程序,这段程序要把自己所有的代码都显示出来。
乍一看觉得这很简单啊,但其实你连一行都显示不了。
比如有这样一个程序,就一行:
这个程序就做一件事情:显示数字100。
问题来了,你如何把“显示(100)”这两个汉字一组括号和一个数字100显示出来呢?
似乎应该这样:
但是其实当你这样做的时候,你已经改变了程序本身,现在的程序为两个“显示”两组括号和一个100,而你运行程序后只能显示一个“显示”一组括号和一个100,很显然你并没有把这个程序全部显示出来。
类似这样的问题,就是计算机无法解决的问题。(有兴趣的朋友可自行百度:停机问题)
2)能够在人类可以容忍的限度内解决的问题。
比如上面的那个“计算1到100内的奇数的和”的问题就是这类问题。解决这类问题所需要的时间的变化是线性变化的。即:“计算1到1000内的奇数的和”所需要的时间是“计算1到100内的奇数的和”的10倍。也就是说问题扩大多少,解决问题所需要的时间就线性地扩大多少。3)无法在人类可以容忍的限度内解决的问题。
这类问题是计算机或者说用这三种逻辑顺序可以解决的、但是所需要的时间是人类无法容忍的。
比如“背包问题”:
一个小偷去博物馆偷东西。博物馆内有3件物品。
第一件物品的重量为3, 价值为4;
第一件物品的重量为2, 价值为3;
第一件物品的重量为4, 价值为5;
小偷的背包最多可以承受的重量为7。请问:应该如何拿物品,可以让背包里的物品总价值最大。
这个问题似乎非常简单,你在稍微比较后就会得出结论:拿第一件和第三件物品。
但是,如果我们扩大一下问题:如果有6件物品、背包可以承受的重量也提高一些,应该怎么拿?
这个时候如果让计算机去解决这个问题,我们就会发现当问题的规模扩大1倍后,计算机所需要的时间却扩大了远不止1倍 —– 即解决问题所需时间不再是线性变化了。
就拿这个问题来说,如果物品数量超过12个(如果我没记错就是12个,反正这个数字很小),那么计算机要想解决这个问题所需要的时间就已经超过了100年。上面的第三类问题,是今天人类在数学和计算机领域的难题,如果大家有兴趣可以了解一下。(自行百度:P问题 NP问题 NPC问题)
======================== BONUS2 =========================
关于8:存储器类型。
8中所涉及的存储器,其实只是硬盘、U盘等存储器的原理。这类存储器的特点是:存放在其中的数据断电后仍然存在,但读数据和写数据都非常慢。
而计算机在运行时会产生很多临时的数据,这些数据只是为当下正在运行的一些程序而服务的,使用计算机的用户并不关心这些数据。相应程序结束或者计算机断电后这些数据就没有存在的必要了。
比如有如下程序:
执行这一行的时候,计算机先计算等号右面的值 —- 结果是3,然后把3存放在一个临时的地方,最后再把这个临时地方里的数值3赋值给sum。(为什么不能直接赋值给sum而要经过一个“临时的地方”:等号右侧的计算,必须在计算机内专门做计算工作的芯片 — 也就是CPU内完成,完成计算后的结果只能保存在CPU的临时存储空间里,然后sum才能拿到这个值)这里的这个“临时存放的地方”,它只是为这个程序而暂时服务一下,过后就不再需要它了。于此同时,我们需要它的读写数据的速度要足够快。如果我们用硬盘来“临时存放这个3”,那么计算机执行这么一行代码也得需要好几秒因为计算机读写硬盘的速度是非常慢的。
因此我们还需要一种存储器:断电后数据不需要存在,但是读写数据的速度要够快。
这种存储器被称为寄存器。寄存器是用触发器实现的而触发器是用上面的4中所提到的各种门实现的。
举一个最简单的例子:
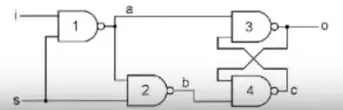
其中,i为这个寄存器的输入,比如如果i是0(1),则表示希望该寄存器存储0(1);o为寄存器的输出,即该寄存器存储的值是多少;s的作用则是“告诉寄存器要工作了”,即当s为1时,寄存器会把i输入的值存储下来 —- 也就是从o输出来。
另外,图中的1、2、3和4为与非门。
与门电路是:两个输入都为1时输出才为1,否则输出均为0。即只要输入有0输出就是0。
与非门电路是:两个输入都为1时输出才为0,否则输出均为1。即只要输入有0输出就是1。
容易想到,与非门电路就是与门电路的输出的地方再接一个非门电路而实现的。假设某个时刻,s是1,i是0,则根据上述与非门的规则,我们可以的到如下结果:
s = 1 i = 0
a = 1 b = 0
c = 1 o = 0
然后,此时我们让s也变成0,同理,可以得出o还是0;再然后,我们让i等于1,得出o还是0。这也就意味着,该寄存器成功保存了当s为1时i的值 —- 也就是0。
同样地,当s和i均为1时,o为1;随后让s为0、i为1和s为0、i为0时,o均为1。也就是说此时寄存器是保存了1(当然还是在s为1时i的值)。
这就是寄存器的大致原理 —- 只要不要断电保持1、2、3和4的正常工作,那么输入即使消失了也会被电路保存下来。
当然,实际的电路要比这个复杂,有兴趣的朋友可以自行阅读相关资料。======================= BONUS3 ======================
关于5:逻辑电路实现四则运算。
我们先来考虑如何实现一位数(二进制)加法。
0 + 0 = 0(无进位:进位为0)
1 + 0 = 1(无进位:进位为0)
0 + 1 = 1(无进位:进位为0)
1 + 1 = 0(有进位:进位为1)
于是问题转化成了:
如何用那些门电路,设计一个逻辑电路,实现上述等号左侧的两个数值为输入,等号右侧的内容为输出(显然,这里需要两个输出,一个是加法结果另一个是进位)?
经过分析不难发现,加法的特点是两个输入一致时结果为0,两个输入不一致时结果为1;同时,只有当两个输入均为1时,进位才为1,其他情况进位均为0。
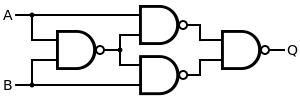
很显然,进位是一个与门电路。而结果呢?则是一种叫异或的逻辑关系:相同为0相异为1。异或门电路有多种实现方式,这里只举一例:只用与非门(BONUS2中已讲过)实现异或门电路:
到此,我们就可以实现上面的一位数的加法了:
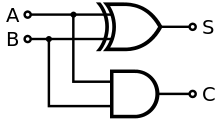
AB为输入,S为加法的结果,C为进位。S的左侧为异或门,C的左侧为与门。
这就是一个半加器。
至于半加器如何做成全加器,这里就不谈了,无非就是把多个半加器串联起来。有兴趣的朋友请自行了解。实现了加法,则可以实现减法,因为减法等效于“加负数”;也可以实现乘法,因为乘法可以转换成多次相加(例如,3 * 3等效于3 + 3 + 3);也可以实现除法,因为除法可以转换成多次相减(例如,7 / 2等效于7 – 2 – 2 – 2:一共减了3次且结果为1,因此7 / 2的结果为:商3余1)。
至此,四则运算全部实现。最后只剩下了一个问题:如何实现负数。
以1和-1为例:
假设我们的加法器可以进行8位二进制的运算,我们用最高位表示符号位:0为正数1为负数。
则1为:00000001-1为:10000001但这样1 + (-1)的结果并不是0,而是10000010,也就是-2。
于是我们需要改变负数的表达方式:按位取反(除了符号位)。
注:我们叫最原始的表达方式为原码,按位取反后的表达方式为反码。正数的反码和原码一样,负数的反码则是原码按位取反后所得。
因此,-1 = (10000001)原 = (11111110)反。
此时,1 + (-1) = (00000001)反 + (11111110)反 = (11111111)反 = (10000000)原 = -0
但这样还有一个问题,就是0和-0的表达方式不同:
0为:00000000而-0为:10000000对负数的反码做进一步处理:加1,形成补码。(正数的补码仍然是原码本身)
1 + (-1) = (00000001)反 + (11111110)反 = (00000001)补 + (11111111)补 = (00000000)补 = (00000000)原 = 0
注:由于一共只能表示8位,所以最后溢出的进位被丢弃掉了。说到这里,一定有朋友会说:
你别急!等一下!你说的这些原码反码补码都是理论,具体到电路中到底是如何实现的呢?
对于这样的问题我就不在这里做详细的解释了,因为它的原理和上面讲的门电路一样,无非就是通过不同的门电路的组合而形成一个复杂但有一定功能的“片子”罢了。(片子是行业黑话,高大上的说法是“芯片”)
以原码变反码为例,其实你可以自己设计一个片子,来实现:
输入是八个0或1,输出也是八个0或1。其中,当最左侧的输入为1时,则其他七位的数字全部取反输出;而如果最左侧的输入为0时,则八个数字全部原样输出。
在这里我仅以一位数字加上符号位(最左侧的位)来简单解释一下:
设符号位为A,输入为B,输出为C。容易得到如下的表(这个表叫真值表,是设计片子的重要手段)
再重复一下:当符号位是0时,数字位原样输出;当符号位是1时,数字位取反输出。
观察真值表可得:当AB相等时C为0,AB不等时C为1。即,相同为0,相异为1 —- 这就是一个异或门了。如何实现异或门上面已经说过了。可见,通过原码求出反码只需要用若干个异或门即可实现。
简单总结一下如何设计电路(这种和01打交道的电路叫做逻辑电路):
第一步:先分析需求,即你要输入什么、输出什么,根据输入和输出,做出真值表;
第二步:观察真值表,找到规律;
第三步:根据上面找到的规律,依据各种门电路的特点,完成逻辑电路的设计。
其中,第二步有的时候会非常复杂,难以一下子找到规律,如果不找规律就直接去设计逻辑电路,那么设计出来的逻辑电路会非常复杂。那么如何解决“找规律难”的问题呢?这就是大学里相关专业的数字电路课程的任务了……这里就不介绍了,如有兴趣,请自行百度:如何通过真值表写出逻辑表达式。我们设计逻辑电路其实就是根据逻辑表达式去做的,故只要确保逻辑表达式已经最简化,那么设计出来的逻辑电路就一定是最简单的。
以上,就实现了整数的四则运算,至于如何实现小数的运算,大同小异,只不过在计算机里是用科学计数法来表示的,在处理上会更加复杂。
====================== 什么是机器思维 =======================
问题一:如果要计算1加到100,应该怎么算呢?
人类:等差数列求和,有公式的:(1 + 100) * 100 / 2 = 5050
机器:愚蠢的人类啊,我们机器最大的长处就是“规律性地计算非常快”,所以我们不需要公式,只需要老老实实从1一直加到100就好了。
问题二:如何判断一个数字是否为偶数。
人类:用这个数字除以2,如果余数为0,则为偶数,否则为奇数。
机器:告诉你,人类,在我这里,/表示除法,%表示求余,我是不是很友好呀?
初级程序员:
机器:呵呵哒,愚蠢的人类,看来即使是程序员也不能真正懂我们的感受!我好伤心,你们知道要我做求余运算需要花多大的力气吗……
高级程序员:
注:按位与运算(与运算:0 & 0 = 0 1 & 0 = 0 & 1 = 0 1 & 1 = 1)
5 & 3 (十进制) = 101 & 011 (二进制) = 001 (二进制) = 1 (十进制)
奇数的二进制的最后一位一定是1,偶数的二进制的最后一位一定是0
机器:眼泪哗哗的!这种位运算我最喜欢啦,因为对我来说最省力最简单了,这样的程序员给我来一打!
最后,送给各位一个小程序:YvesZHI/FallingCode(非程序员请绕行)
体验一下类似“机器表示求余运算很累人”的问题。











