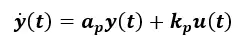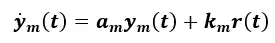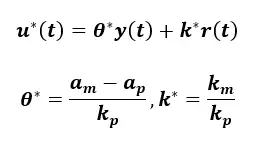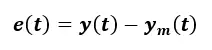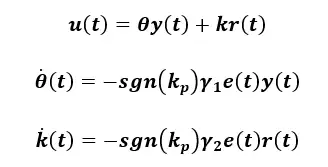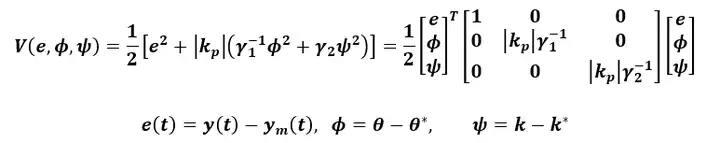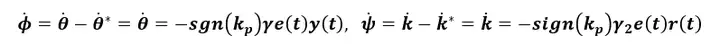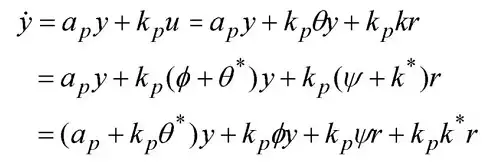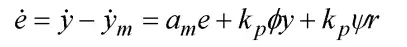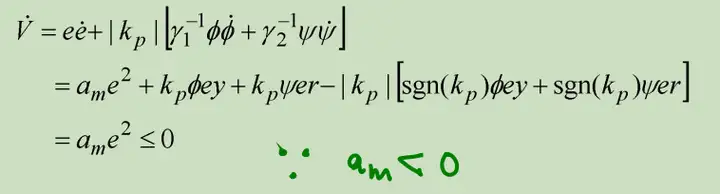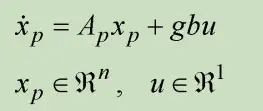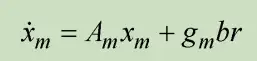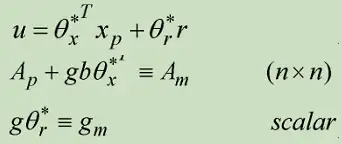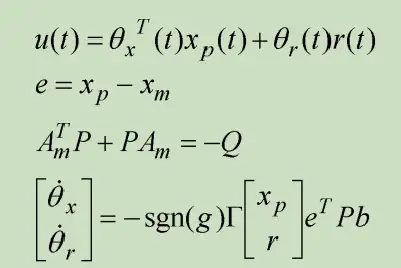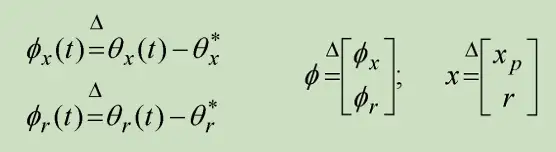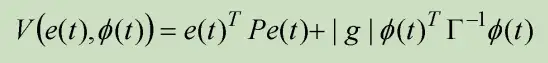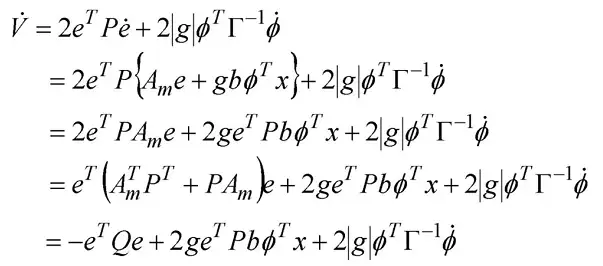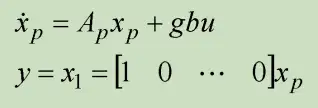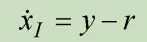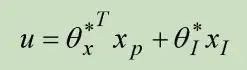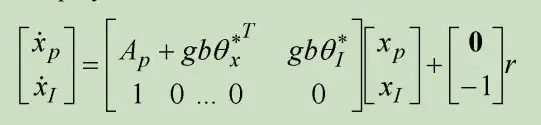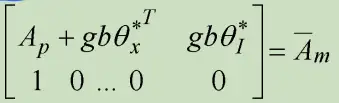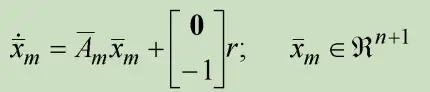最简单的范例
考量两个掌控系统如下表所示
假如他们想那个掌控系统的整体表现和如下表所示参照掌控系统完全一致
假定原掌控系统模块ap,kp未知,能增设掌控律为
消去原掌控系统就能辨认出原掌控系统显得和参照掌控系统完全一致。
但假如原掌控系统模块ap,kp未明呢?这种就难以间接求出θ*和k*
表述掌控系统和参照掌控系统的数值为
这儿得出两个线性的自抗扰律如下表所示
怎样断定那个掌控律能使掌控系统趋于最终目标掌控系统呢?断定操作过程如下表所示
表述有关掌控库季的阿尔布佐夫表达式,只须要断定泊松科夫表达式的有关天数的微分严苛为负,方可断定掌控系统周环平衡。
这儿尽管他们不晓得原掌控系统模块ap, kp,因而也不晓得θ*和k*,但能肯定的使,这些都是常数,于是能得到Φ和ψ的微分
接着考量怎样获得e的微分,将掌控律消去原掌控系统中,能得到
于是能得到
考量阿尔布佐夫表达式的微分,这儿注意到,由于参照掌控系统应当是平衡的,因而am<0
因而掌控库季、掌控模块数值趋近于0
一般情况
考量一般掌控系统
欲使其整体表现为如下表所示参照掌控系统
假定Ap,g,b未知,则能增设掌控律为
假如Ap,g未明,则能增设自抗扰律为
注意,这儿他们须要假定b是完全一致的,而Ap和g是未明的。b未知是两个非常常见的情况,比如开车的时候,将掌控系统简化为两个包含位置、速度、加速度的线性掌控系统,则油门、刹车应当仅影响加速度,即b为[0 0 1]
断定操作过程类似,同样是增设泊松科夫表达式并断定其微分为负。
记
增设泊松科夫表达式为
包含积分掌控的情况
考量一般掌控系统
欲使其整体表现为如下表所示参照掌控系统
考量添加积分掌控以增强掌控系统对抗干扰能力,减小稳态数值,在掌控律中增设数值积分项xI,则有
于是能得到增广掌控系统
假定掌控系统模块未知,可设计掌控律为
得到闭环掌控系统为
记
即参照模型为
这儿须要注意,参照模型的形式并非任意的。
对增广掌控系统和增广的参照模型设计自抗扰律方可
传递表达式形式的自抗扰
断定操作过程十分繁杂,这儿间接得出结果