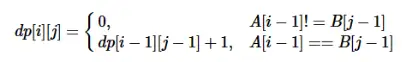一、自学文本
1. 演算法结构设计中四大常见演算法
1) 共管法
结构设计价值观:将两个无法间接化解的大难题降解成体量较细的完全相同难题,以期地方分权。
前述的应用领域:加速次序、福兰县次序
共管法在每几层递回上的基本上关键步骤:
① 降解:将原难题降解为二个体量较细、互相分立、与原难题方式完全相同的子难题。
② 化解:倩女难题体量较细就间接化解,要不然就递回化解各子难题
③ 分拆:将各子难题的解分拆为原难题的解
以加速次序为例认知共管法:
加速次序标识符:
public static void quickSort(int a[],int low,int high){
if(low < high){
int pivotpos = partition(a,low,high);
quickSort(a,low,pivotpos-1);
quickSort(a,pivotpos+1,high);
}
}
public static int partition(int a[],int low,int high){
int pivot = a[low];
while (low < high){
while (low < high && a[high] >= pivot){
–high;
}
a[low] = a[high];
while (low < high && a[low] <= pivot){
++low;
}
a[high] = a[low];
}
a[low] = pivot;
return low;
}
① 降解:选取基准元素,将左右两侧进行划分
② 化解:分别将两个子序列进行加速次序
③ 分拆:将排好的子序列分拆
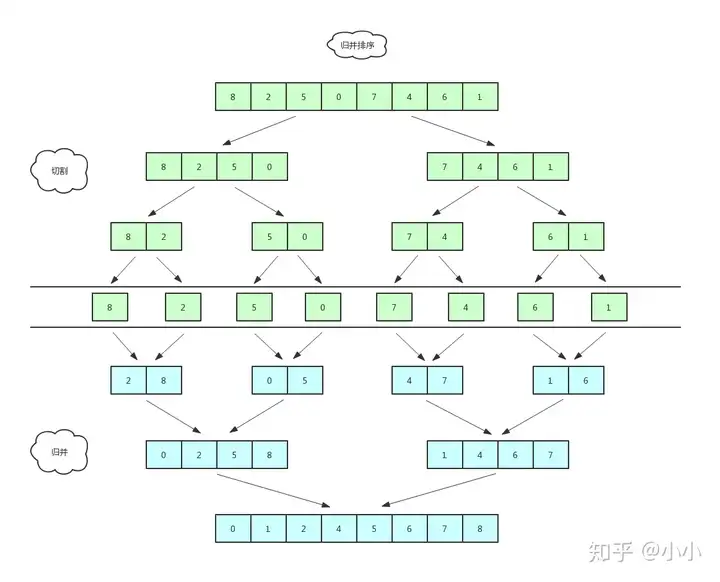
以两路分拆次序为例认知共管法:(共管法中的分拆在福兰县次序中体现得更加清楚)
福兰县次序标识符:
public static void merge(int a[],int low,int mid,int high){
int[] temp = new int[high-low+1];
int i = low;
int j = mid+1;
int k = 0;
while (i <= mid && j <= high){
if(a[i] < a[j]){
temp[k++] = a[i++];
}else {
temp[k++] = a[j++];
}
}
//把左边剩下的移到数组中
while (i <= mid){
temp[k++] = a[i++];
}
//把右边剩下的移到数组中
while (j <= high){
temp[k++] = a[j++];
}
//更新原数组
for (int x = 0;x <temp.length;x++){
a[x+low] = temp[x];
}
}
public static int[] mergeSort(int a[],int low,int high){
int mid = (low+high)/2;
if(low < high){
mergeSort(a,low,mid);
mergeSort(a,mid+1,high);
//左右分拆
merge(a,low,mid,high);
}
return a;
}
① 降解:将两个数组一刀切两半,递回切,直到切成单个元素
② 化解:单个元素分拆成有序的小数组
③ 分拆:小数组分拆成大数组,最终分拆完成
2) 动态规划法
结构设计价值观:最优化原理,即两个过程的最优决策具有这样的性质:即无论其初始状态和初始决策如何,其今后诸策略对以第两个决策所形成的状态作为初始状态的过程而言,必须构成最优策略
动态规划法所要满足的条件:
① 难题中的状态满足最优化原理
② 难题中的状态必须满足无后效性,无后效性指的是下一时刻的状态只与当前的状态 有关而与当前状态的之前状态无关。
动态规划三要素:
① 难题的阶段
② 每个阶段的状态
③ 从前两个阶段转换到后两个阶段的递推关系
前述的应用领域:0/1背包难题 最长公共子串难题
以最长公共子串难题为例认知动态规划法:
定义dp[i][j]表示以A中第i个字符结尾的子串和B中第j个字符结尾的子串的最大公共子串,dp 的大小也为 (n + 1) x (m + 1) ,这多出来的一行和一列是第 0 行和第 0 列,初始化为 0,表示空字符串和另一字符串的子串的最长公共子串。
当我们要求dp[i][j]时,我们要先判断A的第i个元素B的第j个元素是否完全相同即判断A[i – 1]和 B[j -1]是否完全相同,如果相同它就是dp[i – 1][j- 1] + 1,相当于在两个字符串都去掉两个字符时的最长公共子串再加 1;否则最长公共子串取0。所以整个难题的初始状态为:
dp[i][0]=0,dp[0][j]=0
相应的状态转移方程为:
实现标识符:
public static int findLongest(String A,String B){
int n = A.length();
int m = B.length();
if(m == 0 || n == 0){
return 0;
}
int result = 0;
int[][] dp = new int[n+1][m+1];
//初始状态
for(int i = 0; i <= n;i++){
dp[i][0] = 0;
}
for(int i = 0; i <= m;i++){
dp[0][i] = 0;
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
if(A.charAt(i-1) == B.charAt(j-1)){
dp[i][j] = dp[i-1][j-1]+1;
result = Math.max(result,dp[i][j]);
}else {
dp[i][j] = 0;
}
}
}
return result;
}
3) 贪心演算法
结构设计价值观:贪心演算法在对难题求解时,总是做出在当前看来是最好的选择,不从整体最优上加以考虑,它所做出的仅是在某种意义上的局部最优解。贪心演算法不是对所有难题都能得到整体最优解,但对范围相当广泛的许多难题他能产生整体最优解或者是整体最优解的近似解。
前述的应用领域:最小代价生成树之Prim演算法、kruskal演算法 背包难题
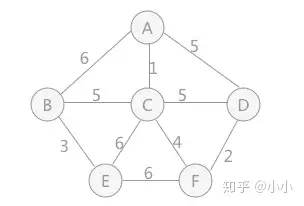
Prim演算法:
在两个无向图中(如上图)找到一棵最小代价生成树,先确定根节点,不断地往上加边,把相关联的节点添加到增长的树上,加边的原则是,连接未在树中并且权值最小的节点
Prim演算法形成的最小代价生成树如下图所示:
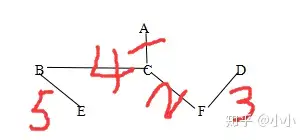
kruskal演算法
kruskal演算法与Prim演算法的区别在于每次都选权值最小的边加入
Prim演算法形成的最小代价生成树如下图所示:
注:上图中标记的数字表示当前边加入的顺序
4) 回溯法
5) 分支限界法
2. 对7.12-7.17的自学文本进行总结
7.12-7.17基本上上是按照计划来进行,进度正常。主要对Java基础部分进行了复习对部分文本加深了认知,主要涉及的内容有集合、线程、Java虚拟机、类间关系的UML表示、IO流、Java对Excel表格的基本上操作,除此以外对MYSQL的多表连接查询进行自学,但是由于没有具体的需求所以并没有写太多具体的SQL,只是利用简单的数据库表对基本上的语法进行了巩固。
另外,对Dubbo框架进行了初步自学,按照官网的介绍创建了两个Dubbo demo,并且 安装了Zookeeper之后成功跑起来。
3. 弄懂TreeSet的两种次序方式
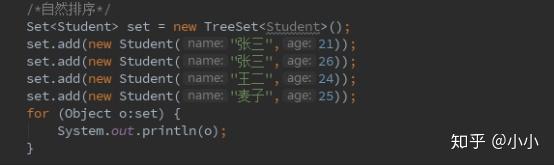
TreeSet是SortedSet接口的实现类,可以确保元素处于次序状态,它有两种次序方式, 自然次序和比较器次序。
① 自然次序:在自定义类中实现Comparerable<T>接口,并且重写compareTo方法
public class Student implements Comparable {
private String name;
private Integer age;
public Student(String name, Integer age) {
this.name = name;
this.age = age;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Integer getAge() {
return age;
}
public void setAge(Integer age) {
this.age = age;
}
@Override
public boolean equals(Object obj) {
if (this == obj)
return true;
if (obj == null)
return false;
if (getClass() != obj.getClass())
return false;
Student other = (Student) obj;
if (age == null) {
if (other.age != null)
return false;
} else if (!age.equals(other.age))
return false;
if (name == null) {
if (other.name != null)
return false;
} else if (!name.equals(other.name))
return false;
return true;
}
@Override
public int hashCode() {
final int prime = 31;
int result = 1;
result = prime * result + ((age == null) ? 0 : age.hashCode());
result = prime * result + ((name == null) ? 0 : name.hashCode());
return result;
}
@Override
public int compareTo(Object o) {
if(o instanceof Student){
Student student = (Student) o;
int i = this.age.compareTo(student.age);
if (i == 0){
return this.name.compareTo(student.name);
}else {
return i;
}
}
return 0;
}
@Override
public String toString() {
return “Student{” +
“name=” + name + \ +
“, age=” + age +
};
}
}
结果:
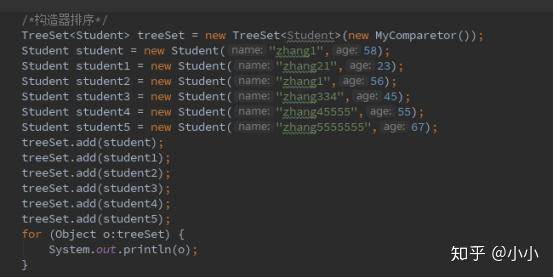
② 比较器次序:在自定义类中实现Comparetor<T>接口,重写compare方法
public class MyComparetor implements Comparator<Student> {
@Override
public int compare(Student o1, Student o2) {
int len1 = o1.getName().length();
int len2 = o2.getName().length();
int num = len1-len2;
int num2 = num == 0 ? o1.getName().compareTo(o2.getName()):num;
int num3 = num2 == 0 ? o1.getAge().compareTo(o2.getAge()):num2;
return num3;
}
}
学生实体不需要实现任何接口,提供构造函数和get set即可
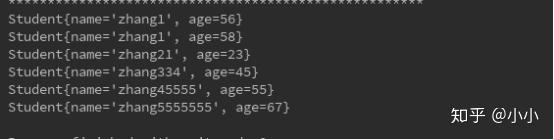
结果:
二、存在的难题
1. 难题化解记录
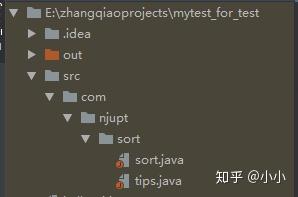
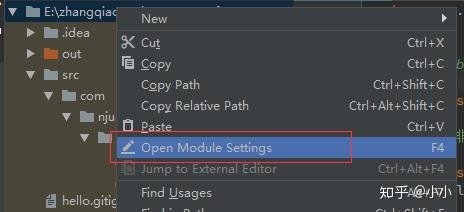
1) 导入两个Java项目,Java文件左下角显示橙色Java图标,项目无法运行,如图所示:
化解办法:
找到父项目,右击选择Open Module Settings
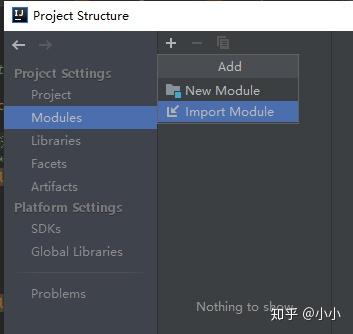
选择Module,点击加号,选择import Module
然后一路Next即可。
三、明天自学计划
1. 建表
2. 继续演算法的自学(回溯法、分支限界法)以及常见的次序演算法