简单谈谈基础的统计学知识 - 网站源码_资源分享

语言学能分成：叙述语言学与推测语言学

一、叙述语言学：使用某一的位数或图象来充分体现统计数据的分散某种程度和对数某种程度。

利用的辅助工具有：平均值值、平均收入、复数、欧几里得平均值值、取舍平均值值、平均数、平均数等。

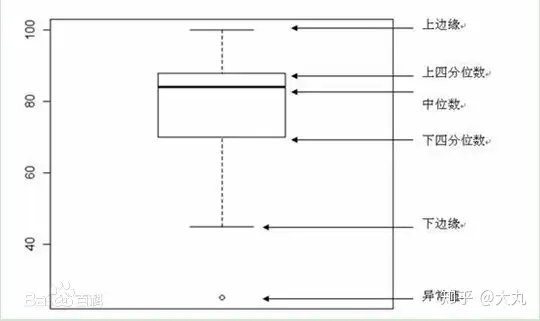
比如说箱技术面就能很好充分反映其中部份重点项目统计统计数据值。

二、推测语言学：依照样品统计数据推测总体的统计数据特点。

较之叙述语言学，大家对推测语言学可能会相对孤单一点。具体来说用两个范例来单纯表明一下为何会有推测语言学。比如说，你想去展开调查西北地区初生女性的平均值体格和运动量，具体来说想不到的最间接的方式是把所有西北初生女性都量测两遍，接着排序出平均值体格和运动量。但此种方式细细再说，虽然间接，但既不可取也不单单。所以另外一类方式是样本，抽出一定数目的西北初生女性展开体格和运动量的量测，接着依照样品的值估计出总体的值。那此种方式利用到的是推测语言学。

推测统计统计数据包括两方面的文本：Bayesian和状态模块。

1、Bayesian：

Bayesian是依照从总体中抽出的样品估计总体分布中包涵的未明模块的方式。它是统计统计数据推测的一类基本形式，分成点估计和区段估计两部份。

还是用如上展开调查西北初生女性体格、运动量的范例，比如说样本量测了10000人的体格运动量，得到10000人的平均值体格、平均值运动量，所以能用10000个样品的平均值体格、平均值运动量来估计总体（整个西北地区初生女性）的平均值体格、运动量。这是两个点估计的范例。

但，需要特别注意，以上范例难让人误会，误以为点估计是完全将总体的排序方式移到样品上展开排序。但事实上，对于每项分项（平均值值、平均数等），样品和总体的排序公式是可能存在差别的。

用样品均值 $x¯$ \bar{x}估计总体均值 $μ$ \mu, $x¯=x1+x2+\dots+xnn$ \bar{x}=\frac{x_1+x_2+\cdots+x_n}{n}

用样品平均数 $s2$ s^2估计总体平均数 $σ2$ \sigma^2, $s2=\sumi=1n(Xi-X¯)2n-1$ s^{2}=\frac{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}}{n-1}

从上两个式子能看出，均值的排序方式在样品和总体上是相同的。但平均数的排序方式，样品平均数排序公司的分子为n-1（样品总数-1），而总体平均数排序公式的分子为N（总体总数）。这个差别单纯来理解能认为是在均值确定的基础上，样品的自由度其实是（n-1）。当然公式也能推理得来，此处不再赘述。但推理过程的基础很重要，值得一提：

点估计的估计量要满足三个要求：无偏性(unbiased)，有效性(efficient)，一致性(consistent)。

无偏性：在重复样本的前提下，所选统计统计数据量的期望值应当等同于真实模块值，即

E(θ^)=θ

E(\hat \theta)=\theta

。

有效性：如果有两个统计统计数据量都是无偏估计量，所以应当选择变异性(variation)最小的那个作为点估计量。

一致性：当样品容量增大时，点估计值应当不断逼近真实的模块值。

前面已经看到，点估计是利用样品统计数据估计出两个具体的数值，所以区段估计是通过样品统计数据，在可信度下前提下得到两个估计的区段。

在具体表明区段估计之前，我们需要明确两个概念，那是总体统计数据的分布会影响样品的分布情况，进而会影响区段估计的分布选择，具体如下表所示：

同样，举例表明，西北初生女性体格范例，我们假设体格符合正态分布、平均数未明，已经样品数目为大样品（10000个），所以此时能选择t分布或者z分布展开估计。

t分布：区段估计公式为： $x¯+tα2σn$ \bar{x}+t_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}

z分布：区段估计公式为： $x¯+zα2σn$ \bar{x}+z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}

其中上两式子中 $x¯$ \bar{x} 为样品均值， $σ$ \sigma 为样品平均数，n为样品数目。 $tα2$ t_{\frac{\alpha}{2}} 和 $zα2$ z_{\frac{\alpha}{2}} 是依照置信度查表得到的值。 $σn$ \frac{\sigma}{\sqrt{n}} 也叫做标准误。

平均数 = 一次样本中个体分数间的对数某种程度，充分反映了个体分数对样品均值的代表性，用于叙述统计统计数据。

标准误 = 多次样本中样品均值间的对数某种程度，充分反映了样品均值对总体均值的代表性，用于推论统计统计数据。

假定总体分布为正态分布，平均数未明。样品数目为11。所以依照上文的表格，应该选定t分布对样品展开估计。

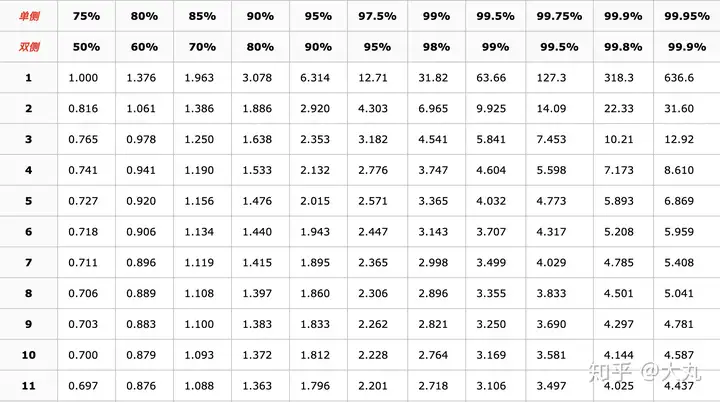
假设样品的均值为1.7，平均数为0.8，置信度为99%，双尾检验。所以查表（置信度99%，自由度为样品数目-1=10，所以查表得到3.169。因此区段估计 $x¯+tα2σn$ \bar{x}+t_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}为（1.7-3.169*0.8/3.3166，1.7+3.169*0.8/3.3166)，其中3.3166为根号11的数值。