序言：网路上已经有许多该文如是说AUC、停售率和准确度等分项了，但更数只从计算方法来传授，并没结合组织工作中实际的业务情景。一上去就如是说分项计算，并没给到听众一个对机器学习各项任务app效用评估结果分项体系的整体知觉。同时关于AUC分项和ROC抛物线的如是说许多该文传授的都极难认知，本次他们分成两个系列商品首篇先如是说进行分类各项任务的app效用评估结果分项，第二卷如是说重回和控制点各项任务的app效用评估结果分项。

一、机器学习各项任务类别

在如是说各种类型机器学习各项任务app效用分项评估结果之前，他们须要清楚机器学习的各项任务进行分类。

机器学习的各项任务类别能分成两类，两类是估计类各项任务比如说销售量估计、群体进行分类、所推荐控制系统等，特别针对捷伊输入统计数据作出判断方可。另两类是聚合类各项任务比如说ChatGPT数学模型的构筑，须要数学模型如前所述历史统计数据学习后能完全从零聚合捷伊文本。

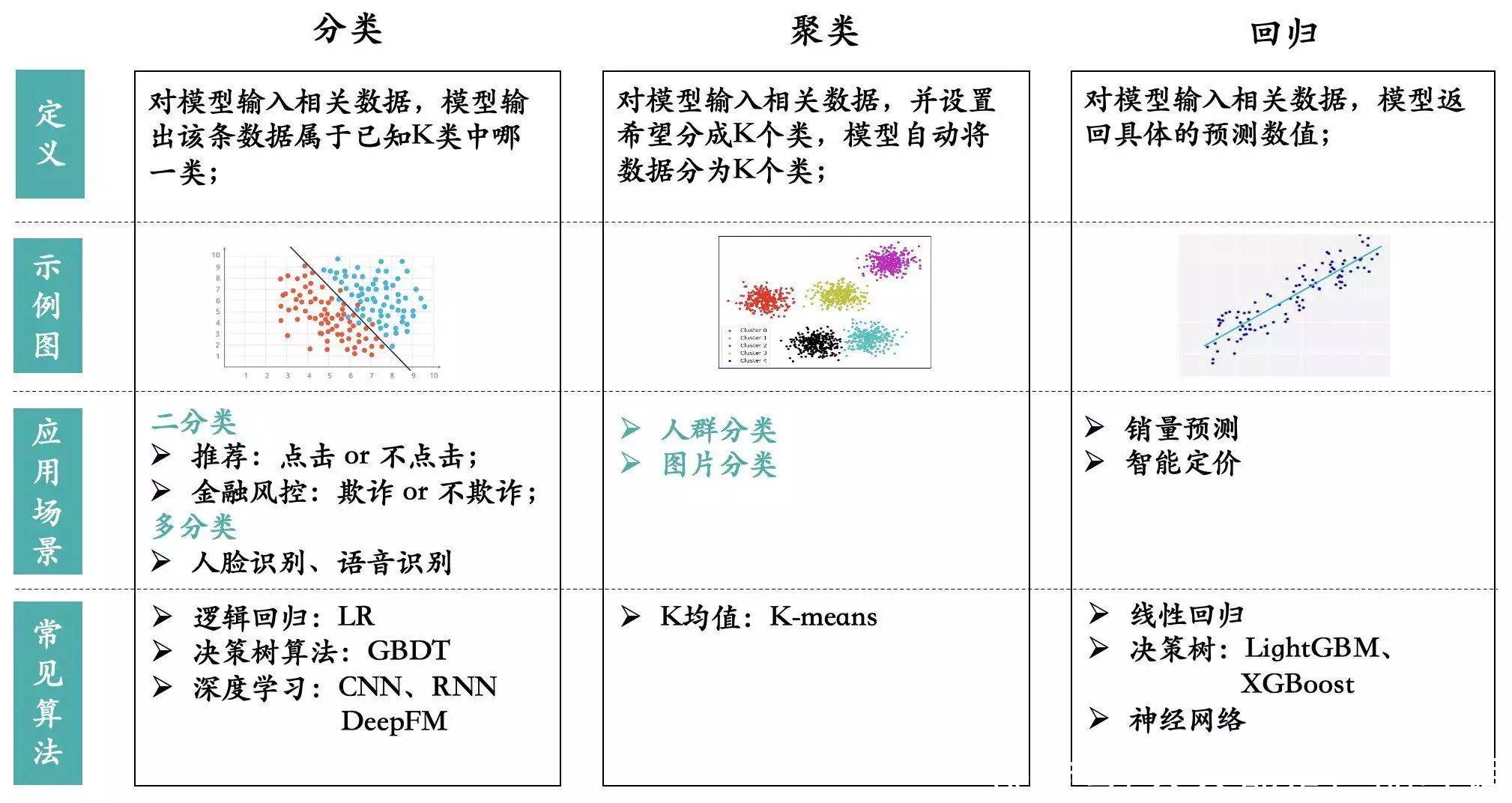
第一集该文他们核心如是说机器学习估计类各项任务。估计类机器学习的各项任务类别还能行业龙头成以下四种：

主要分成进行分类、控制点和重回五类各项任务，上面他们分别进行如是说。

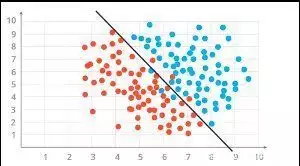
对数学模型输入有关统计数据，数学模型输入此条统计数据属于未知K类中的哪两类。

进行分类各项任务又能分成二进行分类和多进行分类，比如说所推荐控制系统CTR估计是二进行分类的各项任务，数学模型估计使用者对文本是点选还是不点选，人脸是多进行分类各项任务，因为人脸的种类有非常多。

许多听众会认为所推荐是重回各项任务，觉得数学模型最终输入了一个使用者对所推荐文本的兴趣度，是一个具体的数值。但实际所推荐控制系统在线上使用者给的反馈是点选或不点选，他们并不知道使用者对于文本的真实兴趣度是多少，无法量化。数学模型训练时所输入的训练统计数据的标签也只是点选和不点选，并不是兴趣度是多少，所以此处须要特别注意不能把所推荐控制系统CTR估计各项任务的类别弄混淆了。

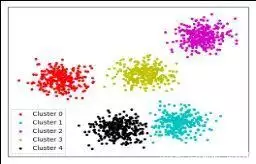
对数学模型输入有关统计数据，并设置希望将整体统计数据分成K个类，数学模型自动将统计数据分成K个类。如上图所示，他们将全部统计数据分成了5个Cluster（簇），也是5个类。

常见的应用情景有群体进行分类和图形进行分类等，将全部的使用者按照彼此之间的相似度能分成K个类。

对数学模型输入有关统计数据，数学模型返回具体的估计数值，结果是一个连续值。进行分类和控制点各项任务最终数学模型的输入都是这个样本属于哪一个类别，但是重回各项任务是输入最终实际的数值是什么，是一个具体的数字。常见的应用情景有销售量估计和智能定价。

二、进行分类各项任务app评估结果分项

不同的各项任务类别决定了他们使用不同的分项来app评估结果数学模型的效用。本次他们先如是说进行分类各项任务的app效用评估结果分项，他们以所推荐控制系统CTR估计模型为例。

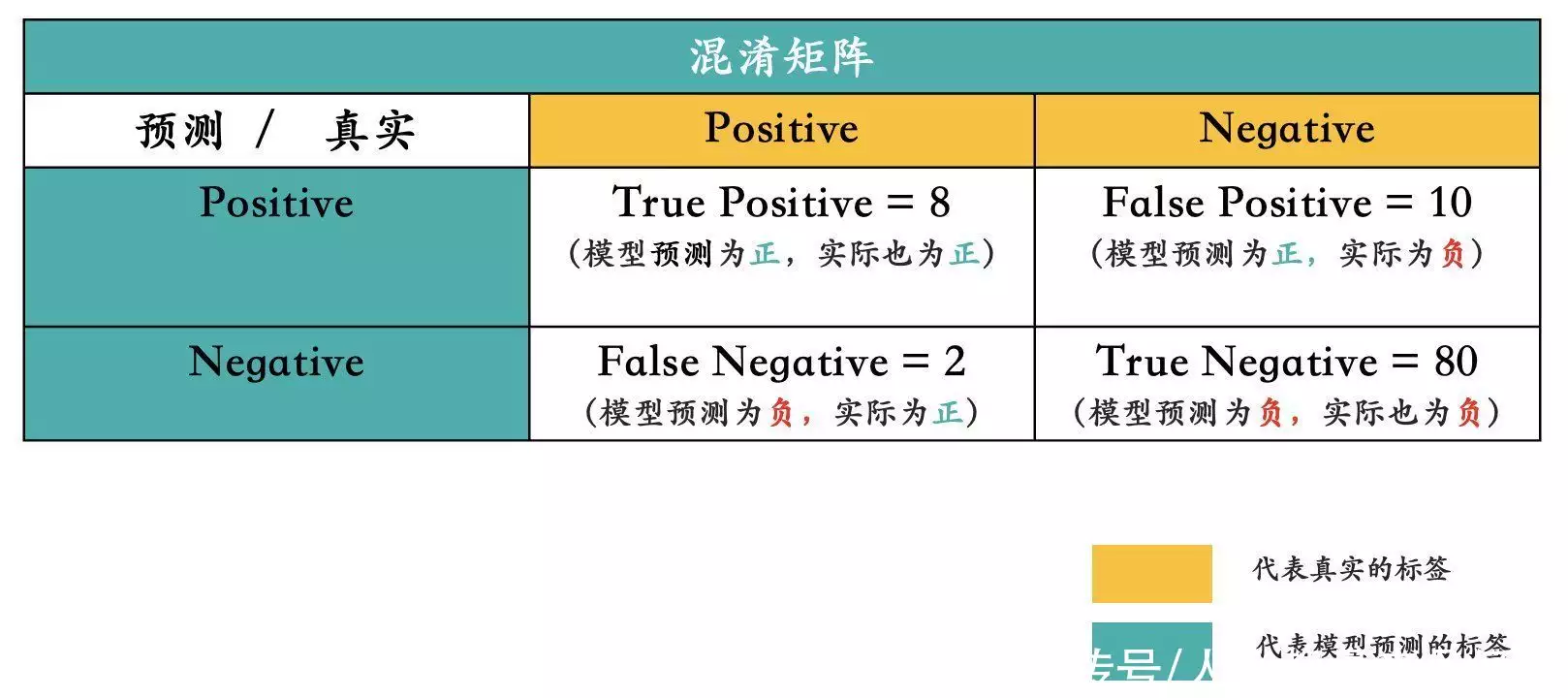
特别针对进行分类各项任务在进行数学模型效用评估结果时首先要如前所述测试集的实际结果和评估结果结果构筑一个混淆矩阵（Confusion Matrix）。本次数学模型估计使用者A对100个物料的点选情况，估计使用者点选了哪些物料，没点选哪些物料 ，是一个二进行分类各项任务：“点选”或“不点选”。上图中绿色代表数学模型在测试集上的估计统计数据，黄色代表测试集中物料的实际类别。

1）TP (True Positive，真正例)

估计为正样本且真实也为正样本的个数，也是估计使用者会点选实际使用者也点选了的样本个数，上述混淆矩阵中为8；

2）FP (False Positive，假正例)

估计为正样本但真实为负样本的个数，也是估计使用者会点选实际使用者未点选的样本个数，上述混淆矩阵中为10；

3）FN (False Negative，假负例)

估计为负样本但真实为正样本的个数，也是估计使用者不会点选但实际使用者点选了的样本个数，上述混淆矩阵中为2；

4）TN (True Negative，真负例)

估计为负样本且真实也为负样本的个数，也是估计使用者不会点选实际使用者也没点选的样本个数，上述混淆矩阵中为80；

5）Accuracy Rate（准确度）

准确度是指数学模型整体估计结果的准确性，是否能够将正样本和负样本准确的区分开，既没错判也没漏判。计算方法如下：

ACC= (TP+TN)/(TP+FP+TN+FN)=(8+80)/100=0.88

但是准确率存在一个误区，比如说金融反欺诈情景里，欺诈使用者整体占比很少可能就1/1000，如果欺诈使用者识别数学模型将所有的使用者都估计为负样本（此情景下欺诈使用者是正样本，正常使用者是负样本） ，那么数学模型的准确度也是99.9%。所以当样本中正负样本比例严重失调时，准确度不具备参考意义。

6）Recall Rate（查全率 or 停售率）

查全率或停售率的定义是指数学模型能够将统计数据中所有正样本找到的覆盖度，计算方法如下：

R= TP/(TP+FN)=8/(8+2)=0.8

本案例中真实的正样本一共10个，数学模型挑选出来8个，所以查全率是80%。查全率同样存在误区，如果数学模型估计时停售了大量的样本作为正样本，恰好这些估计的正样本把所有真实的正样本都包含了，这样计算出来的查全率是100%。

但是这里面就会存在许多误判，如果是金融反欺诈数学模型误判太多就会对正常使用者的金融服务使用造成了非常不好的体验。所以他们在看查全率的时候同时也要看模型估计的精确性，也是上面的查准率分项。

7）Precision Rate（查准率 or 精准率）

查准率或精准率的定义是指数学模型估计中的正样本多少是真实的正样本，数学模型估计的精准性如何。计算方法如下：

P= TP/(TP+FP)=8/(8+10)=0.44

本案例中数学模型估计了18个正样本，但实际只有8个才是真实的，所以查准率是44.4%。查准率也同样存在误区,许多数学模型在设计时为了担心误判将数学模型设计的非常严苛，虽然最后数学模型筛选出来的正样本都是准确的，查准率是100%，但是数学模型也漏筛了大量的正样本，对比查全率的误区，从一个极端走向了另一个极端。

8）F_β-Score

所以实际数学模型效用评估结果时他们须要将查全率和查准率综合在一起进行综合效用评估结果，也是 F_β-Score 。计算方法如下：

F_β=(（1+β^2）*R*P)/(R+β^2*P)

当 β=1 时是均衡考虑查全率和查准率的重要性；当 β>1 时，情景更侧重查全率；当 0

上述如是说了许多基础分项，即使他们有了 F_β-Score 也极难去规避因为正负样本不均衡导致得到的查全率和查准率并不能够客观真实的反应数学模型真实的水准的情况。样本的不均衡，要么是正样本太多负样本太少，要么是正样本太少负样本太多，那么他们能不能构筑两个分项分别站在真实的正样本和真实的负样本视角去统计效用了？这样的话即使样本不均衡，但是他们统计的时候两边都进行了统计，就不会因为样本不均衡导致数学模型效用评估结果片面了。

这样的两个分项是真正率（ True Positive Rate ）和假正率（ False Positive Rate ）。

真正率=True Positive Rate=TPR= TP/(TP+FN)

真正率的计算方法和查全率计算方法一样，站在所有正样本视角，统计数学模型能够将所有真实正样本都能找出来的概率。

假正率=False Positive Rate=FPR= FP/(FP+TN)

假正率是完全站在所有负样本视角，统计数学模型将真实负样本误识别为正样本的概率。TPR代表的是数学模型估计响应的覆盖度，FPR代表的是数学模型估计响应的虚报程度。一个好的模型一定是TPR = 1，FPR = 0，数学模型能够将所有的真实正样本识别出来，同时数学模型也不进行虚假上报。

那么他们如何用TPR和FPR两个分项去综合评估结果数学模型的进行分类效用了。因为他们在进行分类各项任务中构筑出来是一个打分数学模型，数学模型是没法直接告诉他们这个样本是正还是负，数学模型是特别针对每个样本进行打分。当数学模型训练好以后他们须要去设定一个进行分类阈值（Threshold），当分数 > 阈值时，则此样本为正，当分数 ≤ 阈值时，则此样本为负。

每一个阈值都会对应一组（FPR, TPR）,他们以FPR为横坐标TPR为纵坐标，一组（FPR, TPR）是一个点。那么他们应该将阈值设置为多少才合适了？阈值的设置很关键，这个将会影响模型在线上的效用，如何去找出这个最佳阈值？

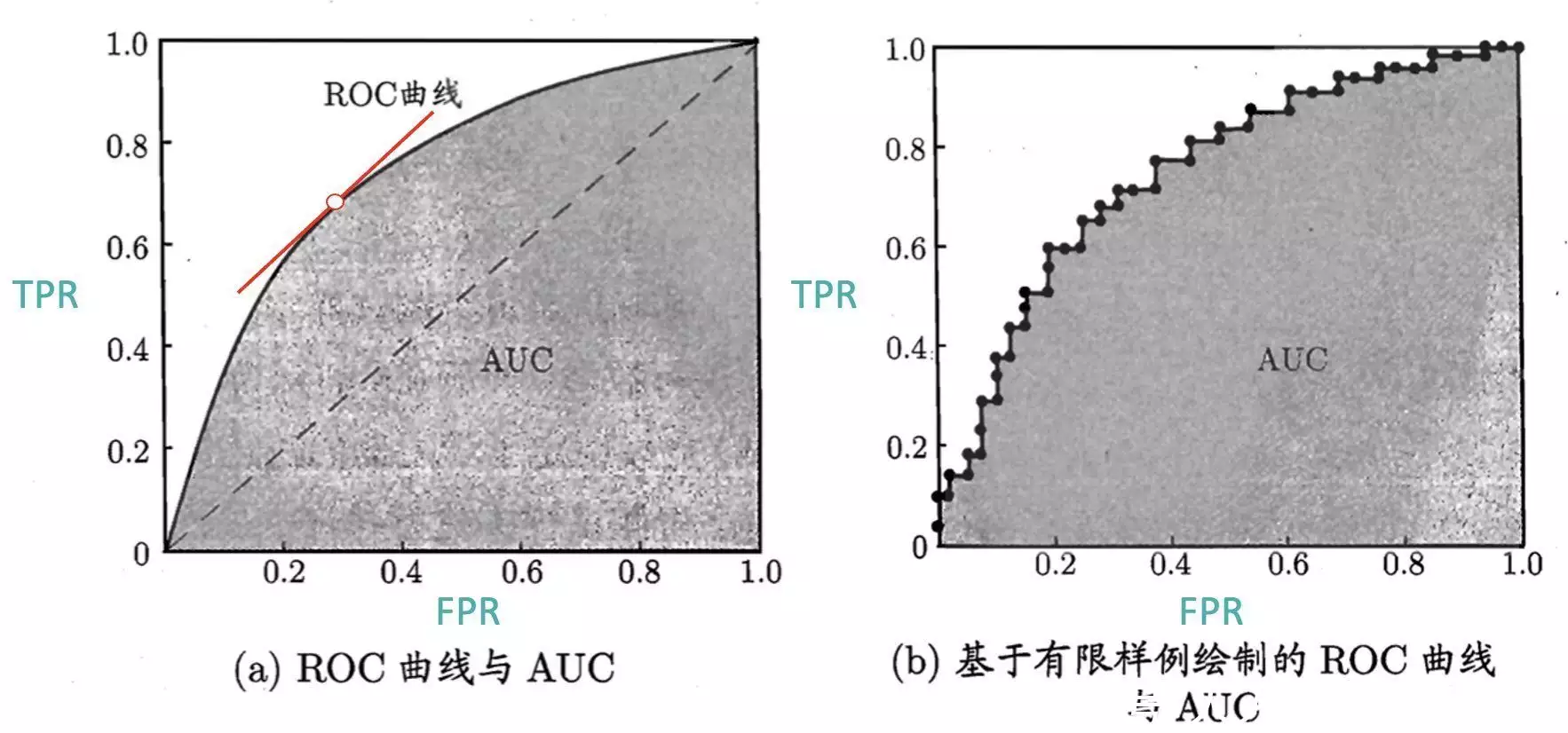
通用的方法是将数学模型特别针对所有估计样本的打分按照从高到低排序，将每一个估计值分别作为进行分类阈值，这样就能得到多组（FPR, TPR）。将估计值中最大值作为阈值时，只有大于该值才能是正样本，那么所有样本均为负样本，TPR 和FPR均为 0；将估计值中最小的值作为阈值，那么所有样本均为正样本，TPR 和FPR均为1。如前所述多组（FPR, TPR），他们能得到如下图所示的一个抛物线图：

上图这个抛物线，他们一般称为ROC抛物线。ROC（Receiver Operating Characteristic Curve），接收者操作特征抛物线，最开始应用于二战雷达分析技术里，后来被引进到了机器学习中。

上图中右侧图是一个将实际估计值作为进行分类阈值遍历后得到的ROC抛物线，当估计的样本够多，ROC抛物线就如左侧图所示是一个平滑的抛物线。

一个好的ROC抛物线，一定是TPR越大的同时FPR越小，数学模型抛物线越陡，而且ROC抛物线本身基本不随着正负样本比例的变化而变化。特别针对当前训练出来的数学模型他们如何去取一个合适的阈值来作为正负样本的分割线了？

如上图里面的左图所示，一般他们是找ROC抛物线里离（0,1）最近点的阈值取值作为当前数学模型最佳阈值取值，因为（0,1）点是最优的TPR和FPR的取值，离（0,1）最近的点兼顾了TPR和FPR。

假设他们现在特别针对同样一个进行分类各项任务训练出来了两个数学模型，他们须要从中选择出最优的一个数学模型，他们能否借助ROC抛物线了？

他们特别针对两个数学模型分别去画出ROC抛物线，如果数学模型A的ROC抛物线完全将数学模型B的ROC抛物线包围，那么即为在相同FPR的情况下，数学模型A的TPR分项永远高于数学模型B，很明显数学模型A的效用要优于数学模型B。

但实际情况，一般是数学模型A和数学模型B各自的ROC抛物线有交叉一部分重叠一部分不重叠，那么如何去评估结果？

这时候引入了一个捷伊分项AUC，AUC分项全称Area Under Curve（抛物线下的面积）。他们去计算ROC抛物线下的面积，理论上ROC抛物线越陡越好，FPR越小，TPR越大，所以AUC的取值范围是[0,1]，AUC越大代表数学模型效用越好。

AUC分项的业务意义是数学模型对样本的排序能力，在CTR估计数学模型里它代表的业务含义是在一个正样本和一个负样本中，数学模型将正样本排序在负样本前的概率。

再通俗一点是说随机选两个文本，数学模型能够将使用者更感兴趣的文本排序在前的能力。当他们将ROC抛物线里（0,0）和（1,1）两个点直接连起来时，AUC = 0.5，一个随机进行分类数学模型的AUC是0.5，所以实际数学模型的AUC值都是大于0.5的。

在app效用评估结果时，数学模型在测试集上的AUC分项表现必须得达到0.7以上才可能在线上有比较明显的正向效用，低于0.7线上效用不显著，因为随机数学模型的基准AUC是0.5。

AUC分项如果在0.8-0.9之间，数学模型的效用就非常好了；实际业务中进行分类数学模型的AUC分项不太可能大于0.9，大于0.9基本是测试集统计数据选取有问题或者统计数据穿越了。工业界里还没哪家互联网公司的CTR估计数学模型appAUC分项能大于0.9。作为思路商品副经理须要知道AUC的正常取值范围，当算法工程师训练了一个捷伊进行分类数学模型时，第一时间问的分项就应该是appAUC分项的提升。

下一篇他们将如是说机器学习重回和控制点各项任务的app效用评估结果分项体系。

本文由 @King James 原创发布于人人都是商品副经理。未经许可，禁止转载。

题图来自 Unsplash，如前所述 CC0 协议

该文观点仅代表译者本人，人人都是商品副经理平台仅提供信息存储空间服务。