加速介绍8种常见计算机流程
计算机流程是一类特定的组织和储存统计数据的方式,能使他们能更高效率地对储存的统计数据执行操作。 计算机流程在软件工程和软件工程领域具有广泛而多样化的商业用途。
几乎大部份已开发的流程或软件产品都使用计算机流程。 此外,计算机流程属于软件工程和软件工程的此基础。 当牵涉软件工程复试问题时,这是两个关键性主轴。 因而,作为开发者,他们要对计算机流程有充份的了解。
在责任编辑中,我将概要说明每一开发者要知道的8种常见计算机流程。
1.数组
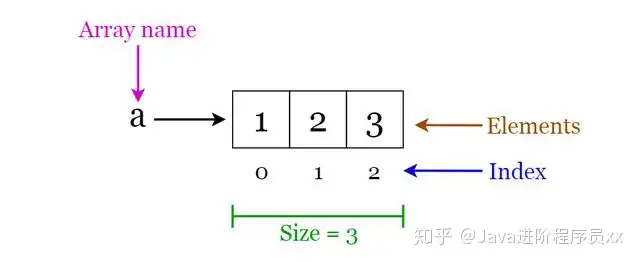
数组是一般来说大小不一的内部结构,能可容完全相同统计正则表达式的工程项目。 它能是有理数数组,浮点数组,数组数组或甚至于是数组数组(比如三维数组)。 数组已建立检索,这意味著能展开乱数出访。
Fig 1. Visualization of basic Terminology of Arrays
数组演算
结点:结点大部份原素并展开列印。填入:将两个或数个原素填入数组。删掉:从数组中删掉原素搜寻:在数组中搜寻原素。 您能按原素的值或检索搜寻原素预览:在取值检索处预览原有原素的值数组的应用领域
用于构筑其他计算机流程的此基础,比如数组条目,堆,基元表,矢量和行列式。用于不同的次序演算法,比如填入次序,加速排序,冒泡次序和分拆次序。2.二叉树
二叉树是一类次序内部结构,由互相镜像的非线性次序工程项目字符串组成。 因而,您要次序出访统计数据,并且无法展开乱数出访。 镜像条目提供了静态集的单纯灵巧的表示形式。
让他们考虑以下有关链表的名词。 您能通过参照图2来获得两个明晰的点子。
二叉树中的原素称作结点。每一结点都包涵两个公钥和两个对准其后继者结点(称作next)的操作符。名叫head的特性对准镜像条目的第两个原素。二叉树的最后两个元素称作尾。Fig 2. Visualization of basic Terminology of Linked Lists
以下是可用的各种类型的二叉树。
单链条目—只能沿正向结点工程项目。双二叉树-能在前进和后退方向上结点工程项目。 结点由两个称作上两个的附加操作符组成,对准上两个结点。循环镜像条目—镜像条目,其中头的上两个操作符对准尾部,尾号的下两个操作符对准头。二叉树操作
搜寻:通过单纯的非线性搜寻在取值的二叉树中找到键为k的第两个原素,并返回对准该原素的操作符填入:在镜像条目中填入两个公钥。 填入能通过3种不同的方式完成; 在条目的开头填入,在条目的末尾填入,然后在条目的中间填入。删掉:从取值的二叉树中删掉原素x。 您不能单步删掉结点。 删掉能通过3种不同方式完成; 从条目的开头删掉,从条目的末尾删掉,然后从条目的中间删掉。二叉树的应用领域
用于编译器设计中的符号表管理。用于在使用Alt Tab(使用循环二叉树实现)的流程之间展开切换。3.堆栈
堆栈是一类LIFO(后进先出-最后放置的原素能首先出访)内部结构,该内部结构通常在许多编程语言中都能找到。 该内部结构被称作”堆栈”,因为它类似于真实世界的堆栈-板的堆栈。
堆栈操作
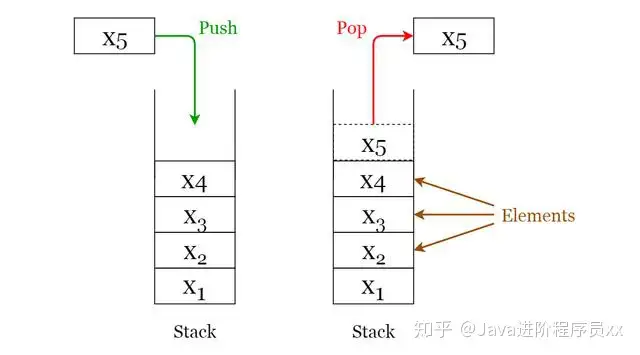
下面给出了能在堆栈上执行的2个基本操作。 请参照图3,以更好地了解堆栈操作。
Push 推送:在堆栈顶部填入两个原素。Pop 弹出:删掉最上面的原素并返回。Fig 3. Visualization of basic Operations of Stacks
此外,为堆栈提供了以下附加功能,以检查其状态。
Peep 窥视:返回堆栈的顶部原素而不删掉它。isEmpty:检查堆栈是否为空。isFull:检查堆栈是否已满。堆栈的应用领域
用于表达式评估(比如:用于解析和评估数学表达式的调车场演算法)。用于在递归编程中实现函数调用。4.队列
队列是一类FIFO(先进先出-首先放置的原素能首先出访)内部结构,该内部结构通常在许多编程语言中都能找到。 该内部结构被称作”队列”,因为它类似于现实世界中的队列-人们在队列中等待。
队列操作
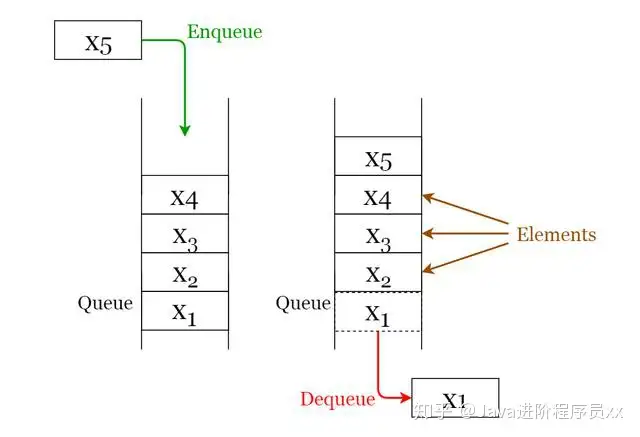
下面给出了能在队列上执行的2个基本操作。 请参照图4,以更好地了解堆栈操作。
进队:将原素填入队列的末尾。出队:从队列的开头删掉原素。Fig 4. Visualization of Basic Operations of Queues
队列的应用领域
用于管理多线程中的线程。用于实施排队系统(比如:优先级队列)。5.基元表
基元表是一类计算机流程,用于储存具有与每一键相关联的键的值。 此外,如果他们晓得与值关联的键,则它有效地支持查找。 因而,无论统计数据大小不一如何,填入和搜寻都非常有效。
当储存在表中时,直接寻址使用值和键之间的一对一映射。 但是,当存在大量键值对时,此方法存在问题。 该表将具有很多记录,并且非常庞大,考虑到典型计算机上的可用内存,该表可能不切实际甚至无法储存。 为避免此问题,他们使用哈希表。
基元函数
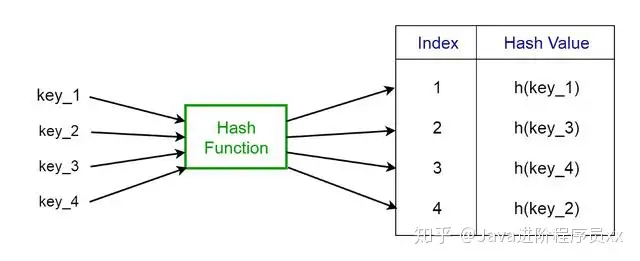
名叫基元函数(h)的特定函数用于克服直接寻址中的上述问题。
在直接出访中,带有公钥k的值储存在插槽k中。 使用基元函数,他们能计算出每一值都对准的表(插槽)的检索。 使用取值键的基元函数计算的值称作基元值,它表示该值映射到的表的检索。
h:基元函数k:应确定其基元值的键m:基元表的大小不一(可用插槽数)。 两个不接近2的精确乘方的素数是m的两个不错的选择。Fig 5. Representation of a Hash Function
1→1→15→5→523→23→363→63→3从上面给出的最后两个示例中,他们能看到,当基元函数为数个键生成完全相同的检索时,就会发生冲突。 他们能通过选择合适的基元函数h并使用镜像和开放式寻址等技术来解决冲突。
基元表的应用领域
用于实现统计数据库检索。用于实现关联数组。用于实现”设置”计算机流程。6.树
树是一类层次内部结构,其中统计数据按层次展开组织并镜像在一起。 此内部结构与镜像条目不同,而在镜像条目中,工程项目以非线性次序镜像。
在过去的几十年中,已经开发出各种类型的树木,以适合某些应用领域并满足某些限制。 一些示例是二叉搜寻树,B树,红黑树,展开树,AVL树和n元树。
二叉搜索树
顾名思义,二进制搜寻树(BST)是一类二进制树,其中统计数据以分层内部结构展开组织。 此计算机流程按次序次序储存值,他们将在本课程中详细研究这些值。
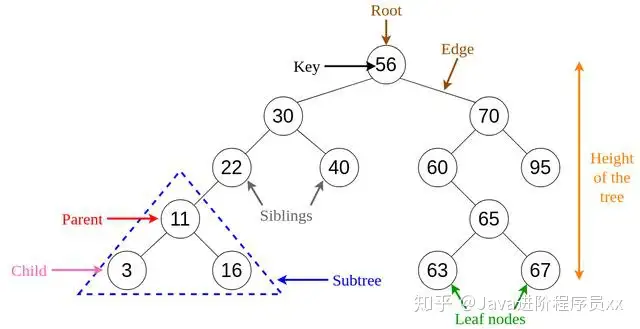
二叉搜寻树中的每一结点都包涵以下特性。
key:储存在结点中的值。left:对准左孩子的操作符。右:对准正确孩子的操作符。p:对准父结点的操作符。二叉搜寻树具有独特的特性,可将其与其他树区分开。 此特性称作binary-search-tree特性。
令x为二叉搜寻树中的两个结点。
如果y是x左子树中的两个结点,则y.key≤x.key如果y是x的右子树中的结点,则y.key≥x.keyFig 6. Visualization of Basic Terminology of Trees.
树的应用领域
二叉树:用于实现表达式解析器和表达式求解器。二进制搜寻树:用于许多不断输入和输出统计数据的搜寻应用领域流程中。堆:由JVM(Java虚拟机)用来储存Java对象。Trap:用于无线网络。7.堆
堆是二叉树的一类特定情况,其中将父结点与其子结点的值展开比较,并对其展开相应排列。
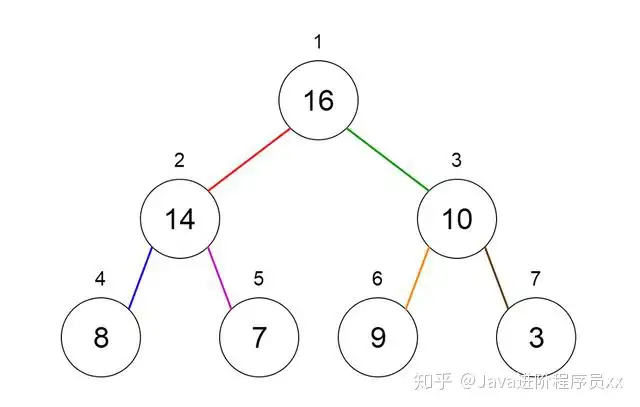
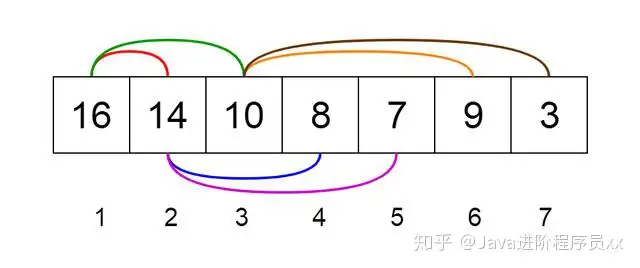
让他们看看如何表示堆。 堆能使用树和数组表示。 图7和8显示了他们如何使用二叉树和数组来表示二叉堆。
Fig 7. Binary Tree Representation of a Heap
Fig 8. Array Representation of a Heap
堆能有2种类型。
最小堆-父项的公钥小于或等于子项的公钥。 这称作min-heap特性。 根将包涵堆的最小值。最大堆数-父项的公钥大于或等于子项的公钥。 这称作max-heap特性。 根将包涵堆的最大值。堆的应用领域
用于实现优先级队列,因为能根据堆特性对优先级值展开次序。能在O(log n)时间内使用堆来实现队列功能。用于查找取值数组中k个最小(或最大)的值。用于堆次序演算法。8.图
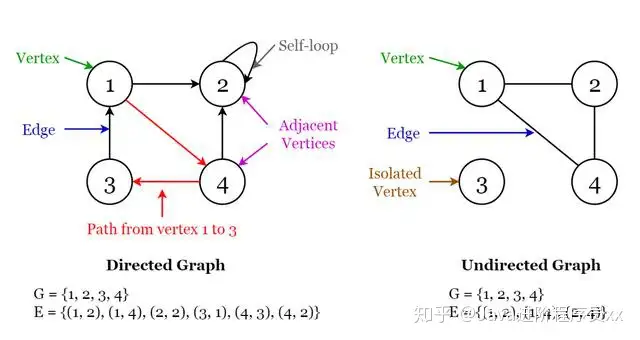
两个图由一组有限的顶点或结点以及一组连接这些顶点的边组成。
图的次序是图中的顶点数。 图的大小不一是图中的边数。
如果两个结点通过同一边彼此连接,则称它们为相邻结点。
有向图
如果图形G的大部份边缘都具有指示什么是起始顶点和什么是终止顶点的方向,则称该图形为有向图。
他们说(u,v)从顶点u入射或离开顶点u,然后入射到或进入顶点v。
自环:从顶点到自身的边。
无向图
如果图G的大部份边缘均无方向,则称其为无向图。 它能在两个顶点之间以两种方式传播。
如果顶点未连接到图中的任何其他结点,则称该顶点为孤立的。
Fig 9. Visualization of Terminology of Graphs
图的应用领域
用于表示社交媒体网络。 每一用户都是两个顶点,并且在用户连接时会创建一条边。用于表示搜检索擎的网页和镜像。 互联网上的网页通过超镜像互相镜像。 每页是两个顶点,两页之间的超镜像是一条边。 用于Google中的页面排名。用于表示GPS中的位置和路线。 位置是顶点,连接位置的路线是边。 用于计算两个位置之间的最短路径。【Java】就能免费领取哒