甚么是斜堆树
取值N个子树做为N个枝叶结点,内部结构一株链表,若该树的为萤方向宽度达至最轻,称这种的链表为最优化链表,也称作斜堆树(Huffman Tree)。斜堆Shahdol为萤方向宽度极短的树,子树较大的结点离根较近。
基本上名词
斜堆树又称为最优化树
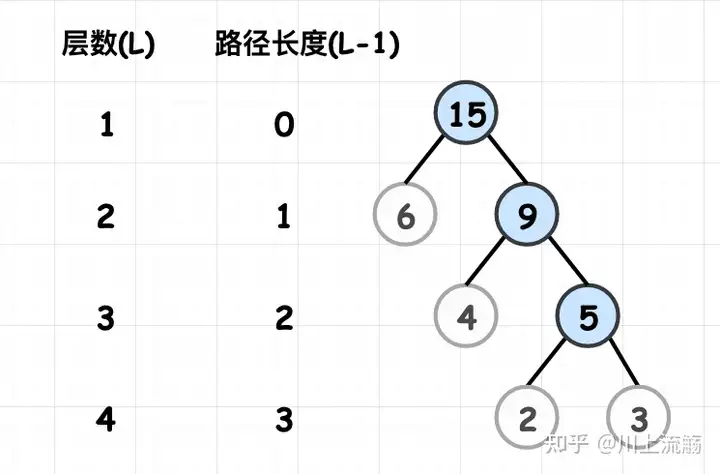
1️⃣ 方向和方向宽度
在一株中,从两个结点往下能达至的小孩或侄子结点间的孔道,称作方向。
孔道中组成部分的数量称作方向宽度。若明确规定根结点的楼层为1,则从根结点到第L层结点的方向宽度为L-1。
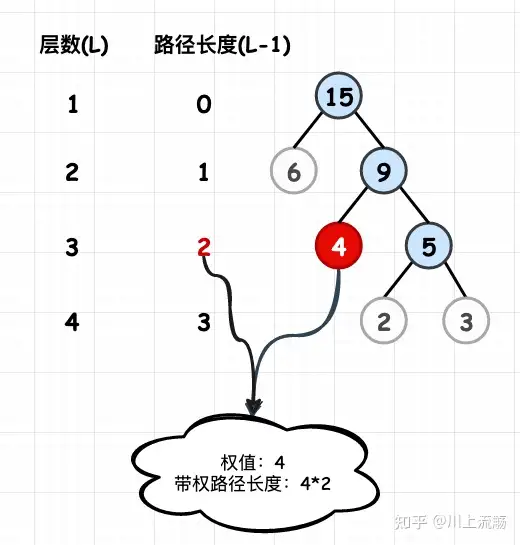
2️⃣ 结点的权和为萤方向宽度
若将树中结点Kozhikode两个有著这种涵义的值,则那个值称作该结点的权。结点的为萤方向宽度为:从根结点到该结点间的方向宽度与该结点的权的平方根。
3️⃣ 树的为萤方向宽度
树的为萤方向宽度明确规定为大部份枝叶结点的为萤方向宽度之和,记作WPL。
示意图:数的为萤方向宽度为:
WPL = (2+3) * 3 + 4 * 2 + 6 * 1 = 29
斜堆树的内部结构
假定有n个子树,则内部结构出的斜堆树有n个枝叶结点。 n个子树依次标为 w1、w2、…、wn,则斜堆树的内部结构准则为:
(1) 将w1、w2、…,wn看作是有n 棵树的丛林(每棵树仅有两个结点);
(2) 在丛林中选出两个根结点的子树最轻的树合并,做为一株新树的左、右子树,且新树的根结点子树为其左、右子树根结点子树之和;
(3)从丛林中删除选取的两棵树,并将新树加入丛林;
(4)重复(2)、(3)步,直到丛林中只剩一株为止,该树即为所求得的斜堆树。
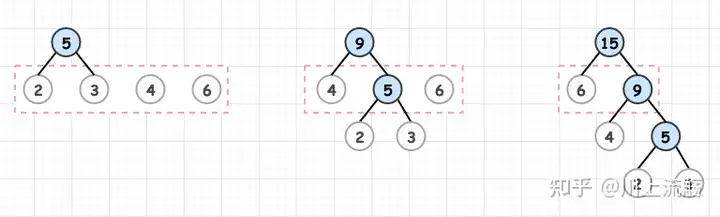
例如:对 2,3,4,6 这四个数进行内部结构
斜堆树的应用:斜堆编码
引言
斜堆编码的介绍斜堆编码是一种压缩编码的编码算法,是基于斜堆树的一种编码方式。斜堆树又称为做为萤方向宽度极短的链表。
斜堆编码跟 ASCII 编码有甚么区别?ASCII 编码是对照ASCII 表进行的编码,每两个字符符号都有对应的编码,其编码宽度是固定的。而斜堆编码对于不同字符的出现频率其使用的编码是不一样的。其会对频率较高的字符使用较短的编码,频率低的字符使用较高的编码。这种保证总体使用的编码宽度会更少,从而实现到了数据压缩的目的。
举两个例子:对字符串“aaa bb cccc dd e”使用 ASCII 进行编码得到的结果为:97 97 97 32 98 98 32 99 99 99 99 32 100 100 32 101 (十进制)需要 16 个字节,如果使用二进制表示的话需要 128位的内存空间去存储。
而如果使用 Unicode 的话会更多,因为 Unicode 又称为作万国码,内容更多,因此使用的空间也需要更大。
接下来使用斜堆编码对上面的字符串进行编码。看看需要多大的空间
统计频率
上面的介绍已经说明了斜堆编码会根据字符出现的频率从而条件字符使用的编码宽度。因此要先求出那个字符串中每个字符出现的频率
字符c 空abde频率443221构建斜堆树
排序斜堆Shahdol两个为萤的链表,而在斜堆编码中,字符的出现频率就是字符的权重。因此要根据字符的频率放入优先队列中进行排序。然后根据这些字符构建一株斜堆树
字符edba 空c频率122344将队列中的每两个元素(字符)都看作一株。
合并进行迭代,每次都去除队列中的前面两个元素,也就是子树最轻的两棵子树进行合并成一株子树。直到最终大部份的元素合并成一株。这棵树就是斜堆树。
合并步骤
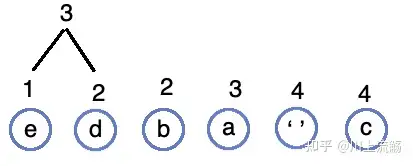
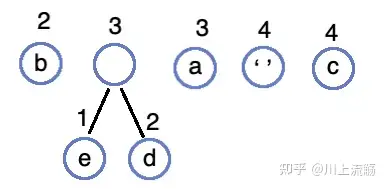
合并 1、2 子树为 3:
将 3这棵树重新插入队列:
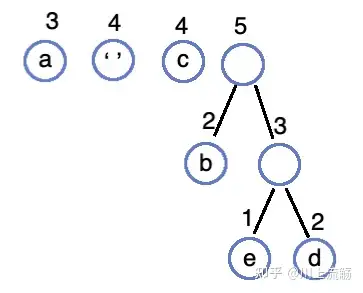
合并 2、3 生成 5 的树,并插入队列:
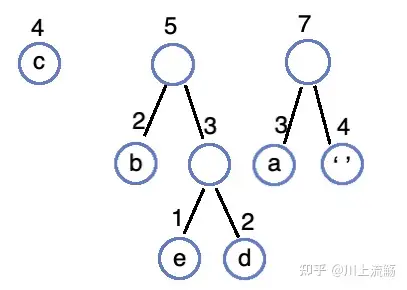
合并 3、4 生成 7 的树,并插入队列:
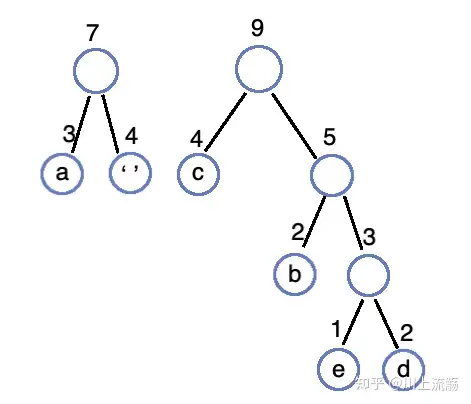
合并 4、5 生成 9 的数,并插入队列:
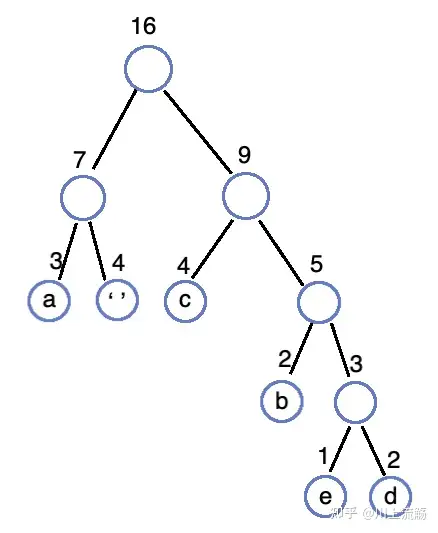
合并 7、9 生成 16 的树,最终只有一株,该树便是那个字符串所生成的斜堆树:
为斜堆树进行编码
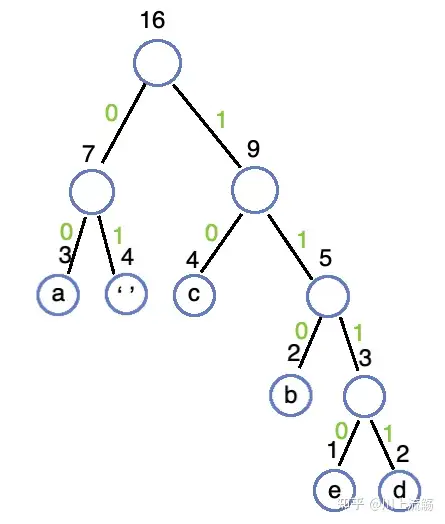
将链表组成部分中的左组成部分编为 0,右组成部分编为 1:
的子结点所经历的方向就是那个字符的编码:
字符edbac编码11101111110000110能发现使用频率高的字符e 其编码宽度是比出现频率低的字符c 编码宽度要少。最后计算使用斜堆编码的字符串“aaa bb cccc dd e”要使用多少位的内存空间进行存储:出现次数 * 编码宽度。结果为 4 * 3 + 3 * 2 + 11 * 2 = 40位,与 ASCII 对应的 128位,少了2/3的存储空间。
相关试题: 3531. 斜堆树 – AcWing题库