链表次序树
链表次序树(BST)
表述
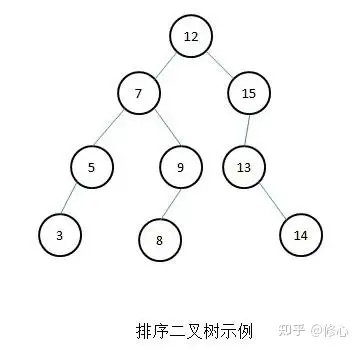
链表次序树又称为链表搜寻树。链表次序树或者一株空树,或者一株具备以下优点的有向链表树:
1)若左结点树有向,则左结点树下大部份结点URL波皮夫大于根结点的URL值。
2)若左结点树非空,则左结点树下大部份结点URL波皮夫大于根结点的URL值。
3)左、左结点树这类也依次是一株链表次序树
左结点树结点值 < 根结点值 < 左结点树结点值,对链表次序树展开前序结点,能获得两个递减的科学规范字符串。
搜寻
二叉次序树的搜寻从根结点已经开始,沿某一组成部分逐级向上展开较为的操作过程。若链表树有向,则将取值值与根结点的URL较为;若成正比,则搜寻获得成功;若以内,则现阶段结点的URL值大于取值URL值时,在根结点的左结点树搜寻,不然在根结点的左结点根上搜寻。这是两个递回的操作过程。
链表次序树的递回搜寻演算法:
BSTNode* BST_Search(BitTree T, ElemType key){
if(T == NULL){
return NULL;
}
if( T->data == key){
return T;
}else if( T->data > key){
return BST_Search(T->lchild, key);
}else if( T->data < key){
return BST_Search(T->rchild, key);
}
}
链表次序树的非递回搜寻演算法:
BSTNode* BST_Search(BitTree T, ElemType key, BSTNode* &p){
p = NULL;
while( T != NULL && key != T->data ){
p = T;
if( key < T->data ){
T = T->lchild;
}else{
T = T->rchild;
}
}
return T;
}
插入
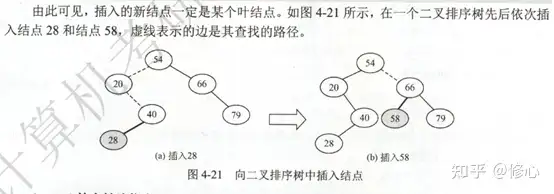
链表次序树是一种动态几何,其特点是树的结构通常不是一次生成的,而是在搜寻操作过程中,当根上不存在URL值等于取值值的结点时在展开插入的。
由于链表次序树是递回表述的,因此插入结点的操作过程如下:若链表次序树为空,则直接插入结点;不然,若URLk大于根结点URL,则插入左结点树,若URL大于根结点URL,则插入左结点树。
bool BST_Insert(BitTree& T, ElemType k){
if( T == NULL){
T = (BitTree*)malloc(sizeof(BitTree));
T->data = k;
T->lchild = T->rchild = NULL;
return true;
}else if( T->data == k){ //根上存在相同URL的结点
return false;
}else if( k < T->key ){
return BST_Insert(T->lchild, k);
}else if( k > T->data ){
return BST_Insert(T->rchild, k);
}
return true;
}
链表次序树的构造
构造一株链表树就是依次输入数据元素,并将它们插入链表次序根上适当位置上的操作过程。具体操作过程:每读入两个元素,就建立两个结点,若链表次序树有向,则将新结点的值与根结点的值作较为,若大于根结点的值,则插入左结点树,不然插入左结点树;若链表次序树为空,则将新结点作为链表次序树的根结点。
void BST_Create(BitTree& T, ElemType str[]){
int sz = sizeof(str)/sizeof(str[0]);
T = NULL;
int i = 0;
while( i < sz ){
Create_BST(T,str[i]);
i++;
}
}
删除(难点)
在链表次序根上删除两个结点时,不能把以结点为根的结点下的结点都删除,必须先把被删除结点从存储链表次序树的链表上摘下,将因删除结点而断开的链表链表重新链接起来,同时确保链表次序树的性质不会丢失。
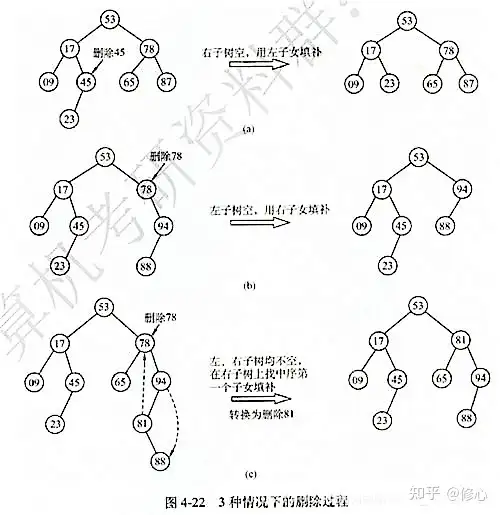
删除操作按三种情况来处理:
若被删除结点 x 是叶结点,则直接删除,不会破坏链表次序树的性质若结点 x 只有一株左结点树或左结点树,则让 x 的结点成为 x 父结点 的结点,替代 x 的位置若结点 x 有左、右两棵结点,则令 x 的直接后继(或直接前驱)替代 x ,然后从链表次序根上删除这个直接后继(或直接前驱),这样就转换成了第一或第二种情况。
//前序结点字符串的下两个结点,即比当前结点大的最小结点,简称后继结点。int successor(BSTTree* p){
p = p->rchild;
while(p->lchild != NULL){
p = p->left;
}
return p->data;
}
//前序结点字符串的前两个结点,即比现阶段结点小的最大结点,简称前驱结点。
int predecessor(BSTTree* p){
p = p->lchild;
while(p->rchild != NULL){
p = p->rchild;
}
return p->data;
}
BSTNode* BST_Delete(BSTTree& T, ElemType x){
if( T == NULL){
return NULL;
}else{
if( x < T->data ){ //要删除的在左边
T->lchild = BST_Delete(T->lchild, x);
}else if( x > T->data ){ //要删除的在右边
T->rchild = BST_Delete(T->rchild, x);
}else{
if( T->lchild == NULL && T->rchild == NULL){//叶子结点
T = NULL;
}else if( T->rchild != NULL){
//如果该结点不是叶子结点且有右结点,则用它的后继结点的值替代,然后删除后继结点 T->data = successor(T);
T->rchild = BST_Delete(T->rchild, T->data);
}else {
//如果该结点不是叶子结点且只有左结点,则用它的前驱结点的值替代,然后删除前驱结点
T->data = predecessor(T);
T->lchild = BST_Delete(T->lchild, T->data);
}
}
}
return T;
}
链表次序树的搜寻效率
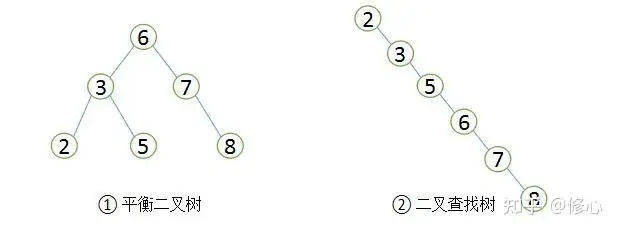
对于高度为h的链表次序树,插入和删除操作的运行时间都是O(h)。但在最坏情况下,构造链表次序树的输入字符串是科学规范的,则会形成两个倾斜的单支树,此时链表次序树的性能新竹变坏,树的高度也增加为元素个数n。
链表次序树的搜寻演算法平均搜寻长度,主要取决于树的高度,即与链表树的形态有关。若退化成链表,则为O(n);若为平衡链表树,则为O(log2n)。
相同的URL其插入顺序不同可能生成不同的链表次序树。
个人主页:
如