宇宙学里的Bootstrap

大背景

前段时间银河系学上有两个路径是采用Bootstrap的方式[1]科学研究银河系学的关连表达式[2]。现代的银河系学是建立在科学研究银河系进化发展史下面的，也是说他们需要找出两个银河系进化发展史，来说明他们看见的现像，比如说红外大背景电磁辐射下面的环境温度差值的关连表达式以及大尺度内部结构上的化学物质原产的关连表达式。他们对银河系的介绍最先根本无法回溯到10−1010^{-10}秒。再向前他们介绍得就较为少了。通常银河系专业委员会假定晚期银河系有两个相对论性的期。那个期银河系会成分股收缩e60e^{60} 倍[3]。那个期银河系是de Sitter内部空间。

科学研究相对论性前夕的力学通常是找两个拉式量，然后用in-in formalism或是Schwinger-Keldysh formalism展开国际标准的相对论性排序，得到相对论性完结的那一关键时刻的等时关连表达式。此种做的缺点原因在于采用了拉式量，因此locality是manifest的。但此种排序有两个缺点，是如果采用拉式量不然会导入太少的redundancy，比如gauge transformation和field redefinition。排序比较复杂，但结论却经常很单纯。如此一来我们就在想，能不能间接从observable起程，去展开bootstrap，而不是采用此种bulk evolution的picture。

只不过在高能量应用领域，现代人早已采用了类似于的方式。比如现代的电动力学科学研究反射增益有三种配套措施。一种配套措施是从拉式量起程展开排序。此种的配套措施就有十分多的redundancy。因此而后现代人合作开发了整套反射增益的排序方式[4]。此种方式的基本原理就从gauge symmetry起程。 如此一来对于许多外腿是无产品质量的反射增益，都可以间接写下国际标准答案了。较为知名的范例是g+g→g+g+gg+g\rightarrow g+g+g此种的过程。如果用现代配套措施，得算25张图。如果用新的反射增益方式是可以间接写下来了。化简了排序。

此种的方式在平直时空里的场论的成功给了现代人generalize到弯曲时空的motivation，也是如何在弯曲时空中做此种bootstrap。这里的核心问题有两个：两个是银河系学的关连表达式需要满足什么样的条件。第二个是银河系学的关连表达式跟反射增益有何关系。那个也是银河系对撞机[5][6]的两个新的科学研究方式。

基础知识

dS内部空间的度规是

ds2=−dη2+dx2(Hη)2\mathrm{d} s^{2}=\frac{-\mathrm{d} \eta^{2}+\mathrm{d} \mathbf{x}^{2}}{(H \eta)^{2}}

在dS内部空间的boundary上 η→0\eta\rightarrow 0 。两个有产品质量的粒子具有如下behavior

limη→0σ(η,x)=O+(x)ηΔ++O−(x)ηΔ−\lim _{\eta \rightarrow 0} \sigma(\eta, \mathbf{x})=O^{+}(\mathbf{x}) \eta^{\Delta^{+}}+O^{-}(\mathbf{x}) \eta^{\Delta^{-}}

其中

Δ±=32±iμ,μ≡m2H2−94\Delta^{\pm}=\frac{3}{2} \pm i \mu, \quad \mu \equiv \sqrt{\frac{m^{2}}{H^{2}}-\frac{9}{4}}

银河系学关连表达式 vs 平坦内部空间反射增益

银河系学上的关连表达式跟反射增益是有联系的。力学上的原因很单纯。原因在于在银河系诞生的极晚期。这些银河系学扰动的模式的波长都远远小于视界的大小。如此一来这些模式是感觉不到内部空间的弯曲的。这时候的物理通常来说是具有洛伦兹对称性的。这时候发生的反射过程的反射增益也会反映到最后的关连表达式下面。

具体是如何联系的可以看下面那个公式

⟨Ok→1⋯Ok→n⟩′∼A′ktpower +c.c.\left\langle O_{\vec{k}_{1}} \cdots O_{\vec{k}_{n}}\right\rangle^{\prime} \sim \frac{\mathcal{A}^{\prime}}{k_{t}^{\text {power }}}+c . c .

公式左边是银河系学上的关连表达式。公式右边是对那个关连表达式做 kt→0k_t\rightarrow 0的展开。leading order的系数是散射增益。

平坦内部空间的反射增益和银河系学关连表达式的类比可以反映在如下几个方面

银河系学关连表达式必须满足的要求

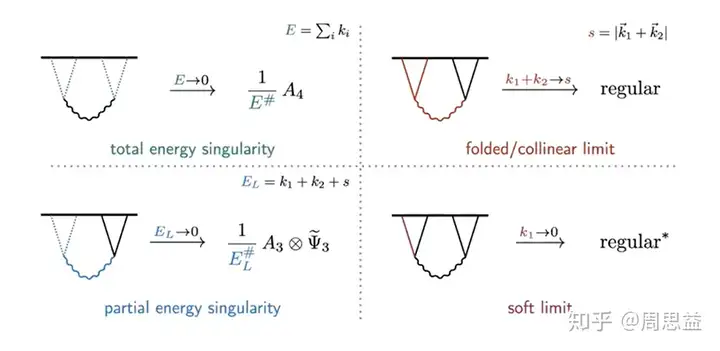
这些是他们知道的银河系学上的关连表达式所具有的一些singularity。根据这些singularity，他们可以fix银河系学关连函数。那个total energy singularity也是前面提到的那个东西。这里那个E→0E\rightarrow 0是平坦内部空间里面的能量守恒的analogue。底下那个partial energy singularity也是类似于的。它的意思是在每个vertex上头都必须满足能量守恒。在那个limit下correlation会factorize。这只不过也是平坦内部空间里面反射增益里面，如果两个传播子on-shell不然，整个反射增益会factorize成两个sub-amplitude的analogue。但这三种singularity都依赖于analytical continuation。右边的folded/collinear limit以及soft limit是physical的，不依赖于analytical continuation。那个folded limit主要是用来看inflation的初始条件的。如果inflation从Bunch-Davis vacuum开始不然，那个limit下correlation就没有singularity。反之，如果inflation从non Bunch-Davis vacuum开始不然，那个limit下correlation就有singularity。但他们通常假定inflation从Bunch-Davis vacuum开始的，因此那个limit下是regular的。另外两个条件是如果外腿取soft limit不然，整个correlation也应该是regular的。

对称性

另外一些对称性的要求也是必须满足的。比如：

第两个对称性现代银河系学里面就知道了，就不多说了。第二个对称性dilatation说明银河系学关连表达式FF 必须满足如下的条件

0=[1+∑nk→n⋅∂k→n]F0=\left[1+\sum_{n} \vec{k}_{n} \cdot \partial_{\vec{k}_{n}}\right] F

简便起见，他们定义两个 F^\hat F

F=s−1F^F=s^{-1} \hat{F}

第三个对称性special conformal说明 FF 必须满足如下条件

0=∑n[k→n(∂k→n⋅∂k→n)−2(k→n⋅∂k→n)∂k→n−2∂k→n]F0=\sum_{n}\left[\vec{k}_{n}\left(\partial_{\vec{k}_{n}} \cdot \partial_{\vec{k}_{n}}\right)-2\left(\vec{k}_{n} \cdot \partial_{\vec{k}_{n}}\right) \partial_{\vec{k}_{n}}-2 \partial_{\vec{k}_{n}}\right] F

产品质量 mϕ=2Hm_{\phi}=\sqrt{2} H 的标量粒子他们称之为conformal coupled scalar。对这些粒子，上述方程有如下的单纯形式

(Δu−Δv)F^=0\left(\Delta_{u}-\Delta_{v}\right) \hat{F}=0

其中

Δu=u2(1−u2)∂u2−2u3∂u\Delta_{u}=u^{2}\left(1-u^{2}\right) \partial_{u}^{2}-2 u^{3} \partial_{u}

uu 和 vv 的定义分别是

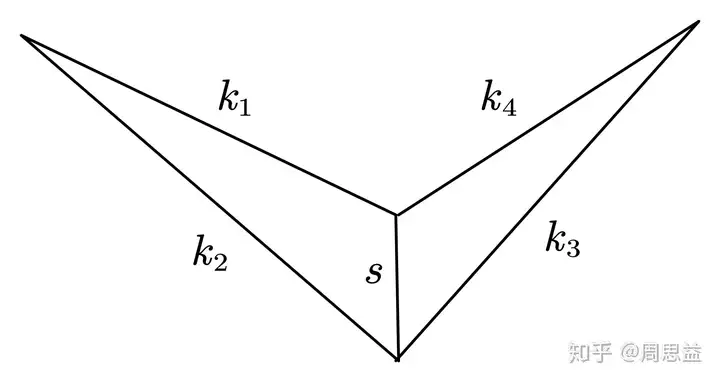
u≡sk1+k2,v≡sk3+k4u \equiv \frac{s}{k_{1}+k_{2}} ~,\quad v \equiv \frac{s}{k_{3}+k_{4}}

ss 的定义如图所示

他们用 C^(u,v)\hat{C}(u, v)来表示上述微分方程的解。

先来考虑最单纯的情况: λφ4\lambda \varphi^4 这时候银河系学关连表达式是

C^0=skt=uvu+v\hat{C}_{0}=\frac{s}{k_{t}}=\frac{u v}{u+v}

如果interaction包含高阶导数，他们可以在前面不断apply那个 Δu\Delta_u 算符得到国际标准答案

C^n≡ΔunC^0=(skt)2n+1f^n(u,v)\hat{C}_{n} \equiv \Delta_{u}^{n} \hat{C}_{0}=\left(\frac{s}{k_{t}}\right)^{2 n+1} \hat{f}_{n}(u, v)

注意上述basis并不能描述积掉的exchange particle是spinning particle的情况。根本无法描述积掉的exchange particle是scalar的情况。

exchange diagram满足的微分方程是

(Δu+M2)F^=(Δv+M2)F^=C^(u,v)\left(\Delta_{u}+M^{2}\right) \hat{F}=\left(\Delta_{v}+M^{2}\right) \hat{F}=\hat{C}(u, v)

其中 MM 是

M2≡μ2+14M^{2} \equiv \mu^{2}+\frac{1}{4}

那个微分方程的解是

F^=∑n(−ΔuM2)nC^M2\hat{F}=\sum_{n}\left(-\frac{\Delta_{u}}{M^{2}}\right)^{n} \frac{\hat{C}}{M^{2}}

那个是两个EFT expansion。但如果用此种series不然，晚期银河系粒子产生的那部分贡献就被扔掉了。因为这部分贡献大约是e−πμe^{-\pi\mu} 。对 Δu\Delta_u 仔细科学研究一番之后发现 F^\hat F满足如下的singularity structure

limu→+1F^∝log⁡(1−u)limu,v→−1F^∝log⁡(1+u)log⁡(1+v)\begin{aligned} \lim _{u \rightarrow+1} \hat{F} & \propto \log (1-u) \\ \lim _{u, v \rightarrow-1} \hat{F} & \propto \log (1+u) \log (1+v) \end{aligned}

经过一番很复杂的排序之后得出 F^\hat F 必须满足如下方程

F^=∑n(−1)n(n+12)2+μ2(uv)n+1+π2cosh⁡πμ(uv)12sin⁡(μlog⁡u/v)μ\hat{F}=\sum_{n} \frac{(-1)^{n}}{\left(n+\frac{1}{2}\right)^{2}+\mu^{2}}\left(\frac{u}{v}\right)^{n+1}+\frac{\pi}{2 \cosh \pi \mu}\left(\frac{u}{v}\right)^{\frac{1}{2}} \frac{\sin (\mu \log u / v)}{\mu}

那个方程的第一项是EFT项。第二项是对应于particle production的项。

由此就可以从对称性以及singularity来fix银河系学关连表达式的形式。

参考