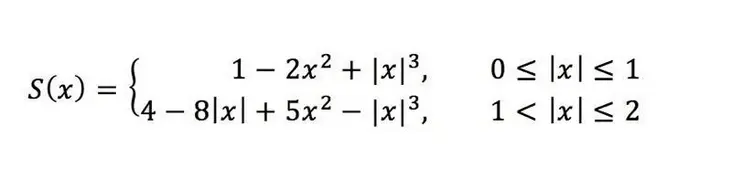在采用 OpenCV 的 resize 表达式时,存有对数类别的ZWG,如 INTER_NEAREST(前段时间邻对数)、INTER_LINEAR(双非线性对数)、INTER_CUBIC(双四次对数)等。在此做个历史记录。
双非线性对数
以水准路径 y→\vec{y} 路径为例,做一场非线性对数,非线性满足用户上式
f(y2)−f(y1)y2−y1=f(y)−f(y1)y−y1\frac{f(y_2) – f(y_1)}{y_2 – y_1} = \frac{f(y) – f(y_1)}{y – y_1}
则能获得最终目标点 yy 的对数结论,
f(y)=(y2−y)⋅f(y1)+(y−y1)⋅f(y2)f(y) = \color{red}{(y_2 – y)} \cdot f(y_1) + \color{red}{(y – y_1)} \cdot f(y_2)
一般满足用户 y1≤y≤y2,y2=y1+1y_1 \leq y \leq y_2,\,\,\,y_2 = y_1 + 1 ,
上面的对数直观理解, yy 离 y2y_2 越近, (y2−y)(y_2 – y) 越小, f(y1)f(y_1) 的权重越小, yy 和 y1y_1 的 ff的表达式值越不相近;而(y−y1)=(y−(y2−1))=1−(y2−y)(y – y_1) = (y – (y_2 – 1))= 1 – (y_2 – y) 越大, f(y2)f(y_2) 的权重越大, yy 和 y2y_2 的 ff 的表达式值越相近,合理。
同理,能获得竖直路径 x→\vec{x} 的非线性对数
f(x2)−f(x1)x2−x1=f(x)−f(x1)x−x1\frac{f(x_2) – f(x_1)}{x_2 – x_1} = \frac{f(x) – f(x_1)}{x – x_1} ,
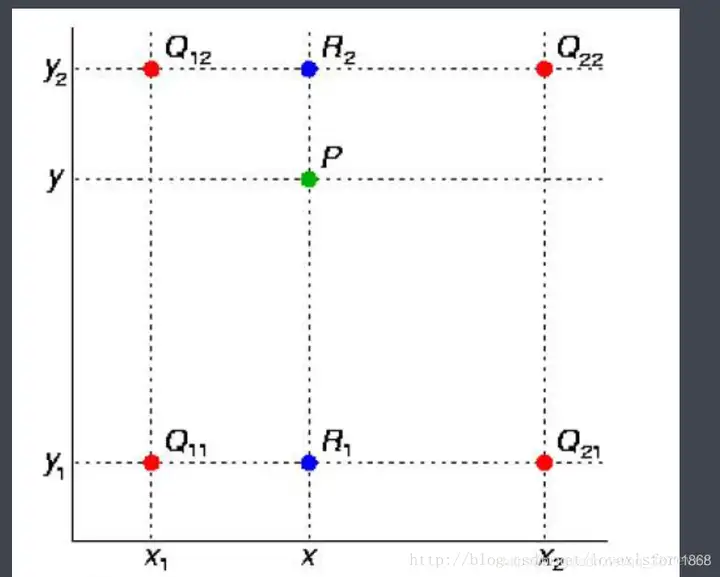
双非线性对数能看作是先在水准路径做两次非线性对数,再在竖直路径上对前面的两个对数结论做一场非线性对数,具体如下图,
上图中, Q12Q_{12} 和 Q22Q_{22} 做一场非线性对数获得 R2R_2 ,然后 Q11Q_{11} 和 Q21Q_{21} 做一场非线性对数获得 R1R_1 ,最后 R2R_2 与 R1R_1 做一场非线性对数获得最终目标坐标 PP的值(PP 是小数的坐标,不是离散的)。
(注:先在竖直路径上做,再水准路径做,二者是等价的)。
下采样
先以下采样为例
假如要将 5×55\times 5 的图像 II 对数成 3×33 \times 3 的图像 OO,以水准方向y→\vec{y} 为例,按照水准的宽比 53=1.67\frac{5}{3} = 1.67 ,求最终目标图像 OO 中 (0,1)(0, 1) 的点,对应输入图像 II 中坐标 (0,1.67)(0, 1.67),表示为PP,则找到 PP 周围四个点—— (0,1),(0,2),(1,1),(1,2)(0,1),(0,2), (1,1), (1,2) ,根据距离的大小做加权(之前的非线性对数),获得坐标 PP 处的值,即
f(P)=0.33⋅f(0,1)+0.67⋅f(0,2)+0⋅f(1,1)+0⋅f(1,2)f(P) = 0.33 \cdot f_{(0,1)} + 0.67 \cdot f_{(0,2)} + 0 \cdot f_{(1,1)} + 0 \cdot f_{(1,2)} 。
同理,如果求最终目标图像中点 QQ (1,2)(1,2) 的值,对应原图 5×55\times 5 中的坐标为 (1.67,3.33)(1.67, 3.33) ,找到周围四个点 (1,3),(1,4),(2,3),(2,4)(1, 3),(1, 4), (2, 3), (2, 4) ,做四次非线性对数——先水准路径做两次非线性对数,分别获得
f(R2)=0.67⋅f(1,3)+0.33⋅f(1,4)f(R_2) = 0.67\cdot f_{(1,3)} + 0.33 \cdot f_{(1,4)}
f(R1)=0.67⋅f(2,3)+0.33⋅f(2,4)f(R_1) = 0.67\cdot f_{(2,3)} + 0.33 \cdot f_{(2,4)}
获得的两个值,再在竖直路径做一场非线性对数
fQ=0.33⋅f(R2)+0.67⋅f(R1)f_{Q} = 0.33\cdot f(R_2) + 0.67 \cdot f(R_1)
即可。
居中
下采样演算法按照上面的演算法,能获得一个下采样结论,但对数时会忽略右下角的内容,还是上面 5×55\times 5的图像II 对数成 3×33 \times 3 的图像 OO,在水准 y→\vec{y} 路径上,求解 II 每一个点对应原图 OO 的 yy 坐标如下
0,1.67,3.330,\,1.67,\,3.33
竖直 x→\vec{x}方向同理,坐标是0,1.67,3.330,\,1.67,\,3.33
但原图 II 的坐标范围是 y→\vec{y} ~[0,4][0, 4] 和 x→\vec{x} ~[0,4][0,4]
能发现,对数时只会利用到原图OO 左上角的像素,右下角的内容被忽略掉了。
如果换成更大图像的下采样,比如 120×120120 \times 120 的图像下采样为 3×33\times 3 ,两个路径都只会利用到 0,40,800, 40, 80 这些坐标的值,而忽略掉了 81−11981 -119 坐标的内容,这样的下采样有点不合格。
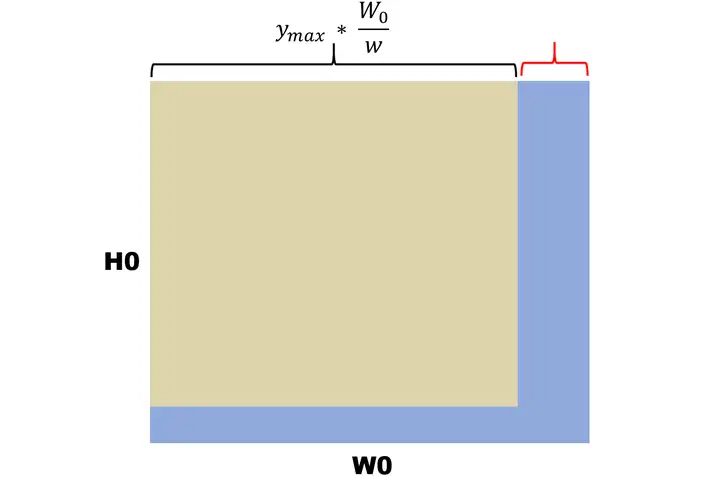
因此,后面提出将两幅图像的中心对齐,如下图
求解 h×wh\times w的小图,因为坐标都是从 0 开始的,所以在水准y→\vec{y} 路径上最远能到达 (w−1)⋅W0w(w – 1) \cdot \frac{W_0 }{w} ,则右侧有
(W0−1)−((w−1)⋅W0w)=W0w−1\begin{aligned} &(W_0 – 1) – \big((w – 1)\cdot \frac{W_0}{w}\big) = \frac{W_0}{w} – 1 \end{aligned}
空出来了,将上图黄区域往右偏移12\frac{1}{2} 个空出来的距离,即可尽量利用到中间的信息。
原来从小图映射到大图的坐标计算是
y×W0wy \times \frac{W_0}{w} ,
现在往右偏移
y×W0w+12×(W0w−1)y \times \frac{W_0}{w} + \frac{1}{2} \times \big( \frac{W_0}{w} – 1 \big)
化简一下,
(y+0.5)×W0w−0.5(y + 0.5) \times \frac{W_0}{w} – 0.5 ,
同理 xx 路径上小图映射到大图的坐标计算就是
(x+0.5)×H0h−0.5(x + 0.5) \times \frac{H_0}{h} – 0.5
上采样
下采样没什么问题,但上采样有所不同(以下只是我个人的看法,没看源码也看权威实现)。
举个例子, 3×33 \times 3 的图像放大为 5×55 \times 5的图像,如果按照下采样的思路(先不考虑中心对齐),获得的一个路径上的坐标有
0,0.6,1.2,1.8,2.40, 0.6, 1.2, 1.8, 2.4
一共五个坐标,但最后的坐标 2.42.4 超出了原图 3×33 \times 3在一个路径的坐标范围——(0,0),(0,1),(0,2)(0, 0), (0, 1), (0, 2) ;
再假如是,3×33 \times 3 的图像放大为 7×77 \times 7的图像,一个路径的坐标就有
0,0.429,0.857,1.285,1.714,2.143,2.5710 \color{red}{ , }0.429\color{red}{ , }0.857\color{red}{ , }1.285\color{red}{ , } 1.714\color{red}{ , }2.143\color{red}{ , }2.571
有两个坐标 2.143,2.5712.143\color{red}{ , }2.571 超出了原图的坐标范围,也不可取。
因此,我修改一下坐标映射
y×W0−1wy \times \frac{W_0 – 1}{w}
然后以上采样为 7×77 \times 7 为例, y×3−17y \times \frac{3 – 1}{7} ,一个路径上从 0, 1, 2, 3, 4, 5, 6的七个坐标有
0,0.285,0.571,0.857,1.1428,1.428,1.7140\color{red}{,}0.285\color{red}{,}0.571\color{red}{,}0.857\color{red}{,}1.1428\color{red}{,}1.428\color{red}{,}1.714
右下角也没利用到,再和之前一样做个中心对齐,
y×W0−1w+12×(W0−1w−1)=(y+0.5)×W0−1w−0.5y \times \frac{W_0 – 1}{w} + \frac{1}{2} \times \big( \frac{W_0 – 1}{w} – 1 \big) = (y + 0.5) \times \frac{W_0 – 1}{w} – 0.5
除了上面写的一个可能可行的方案,还有另一种办法,不做中心对齐,
直接坐标映射改成 y×W0−1w−1y \times \frac{W_0 – 1}{w – 1} ,以 3×33 \times 3 的图像放大为 7×77 \times 7 的图像为例,拉伸比变成了
37→3−17−1=26=0.33\frac{3}{7} \rightarrow \frac{3 – 1}{7 – 1} = \frac{2}{6} = 0.33 ,
一个路径上从 0, 1, 2, 3, 4, 5, 6的七个坐标有
0,0.33,0.67,1.0,1.33,1.67,20\color{red}{,}0.33\color{red}{,}0.67\color{red}{,}1.0\color{red}{,}1.33\color{red}{,}1.67\color{red}{,}2
恰好布满原图像 3×33 \times 3在一个路径上的区间范围!而且不需要做中心对齐。
上面都是两个路径都是同时放大,或者同时缩小,如果一个路径拉伸,另一个路径缩小,就分别采用上采样的映射和下采样的映射即可。
实验
341 x 512下采样
140 x 200上采样
1600 x 2400代码
BiCubic 对数
双立方对数,原理看得我有点混乱,我也是在网上胡乱搜,好多博客都是直接给一个定义好的局部 4×44 \times 4 加权表达式,比如
至于为什么,有论文,但我没去看。我选择了一种更简单的理解方式,源于这个博客,直接从一维的 cubic 出发,给定 4 个连续点,求解四次表达式 f(x)=ax3+bx2+cx+df(x) = ax^3 + bx^2 + cx + d 的四个参数 a,b,c,da,b,c,d ,就可估计出映射坐标下界从 [-1, 2] 内的任意点的值,原理如下:
原理
Cubic 对数
f(0)=df(1)=a+b+c+df′(0)=f(1)−f(−1)2f′(1)=f(2)−f(0)2\begin{aligned} f(0) &= d \\ f(1) &= a + b + c + d \\ f(0) &= \frac{f(1) – f(-1)}{2} \\ f(1) &= \frac{f(2) – f(0)}{2} \end{aligned}
这里直接用 f(x+1)−f(x−1)2\frac{f(x + 1) – f(x – 1)}{2} 近似获得 f′(x)f(x),当然也能采用更加精确的近似方法。上面四个方程f(−1),f(0),f(1),f(2)f(-1), f(0), f(1), f(2) 已知,求 a,b,c,da,b,c,d ,如下:
a=−0.5∗f(−1)+1.5∗f(0)−1.5∗f(1)+0.5∗f(2)b=f(−1)−2.5∗f(0)+2∗f(1)−0.5∗f(2)c=−0.5∗f(−1)+0.5∗f(1)d=f(0)\begin{aligned} a &= -0.5 * f(-1) + 1.5 * f(0) – 1.5 * f(1) + 0.5 * f(2) \\ b &=f(-1) – 2.5 * f(0) + 2 * f(1) – 0.5 * f(2) \\ c &= -0.5 * f(-1) + 0.5 * f(1) \\ d &= f(0) \end{aligned}
举个例子,
假如映射坐标是 3.23.2 ,获得下界 floor(3.2)=3floor(3.2) = 3 ,从坐标 33 开始,偏移量 [−1,2][-1,2] 之内的对数表达式能用上面的 f(x)f(x) 来近似,只要知道 f(−1),f(0),f(1),f(2)f(-1), f(0), f(1), f(2) 四个偏移量上的灰度值,就能估算出偏移量 [−1,2][-1,2] 内每一个点的值,例如 f(3.2)f(3.2)
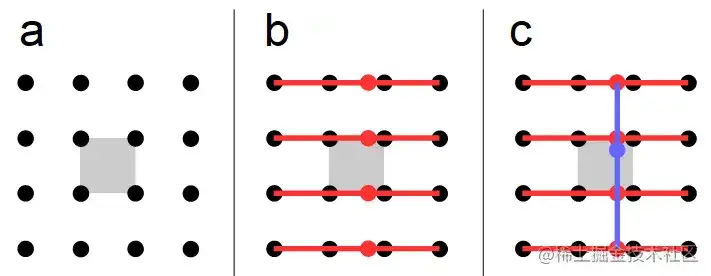
拓展到二维,就是 bicubic,能先水准路径 cubic 对数获得四个值,获得的四个值在竖直路径上再做一场 cubic 对数获得映射坐标的灰度值,如下图
实验
原图 314 x 512先双立方对数缩小图像
双立方对数 50 x 75再对数放大图像
我写的双非线性对数 600 * 900我写的双立方对数OpenCV 的双立方对数双立方对数,我暂时没看出来哪里更好,可能是我写错了,但是我采用 OpenCV 内置的 INTER_CUBIC 也获得了不是很好的效果,看样子这种情况下还是需要超分辨适合一点。
代码
C++, 双立方对数即使开了 O2 也很慢,毕竟是 16 个点参与对数计算。
实现细节上,和之前的双非线性对数一样,映射之后的坐标偏左上方,需要求右边、下面空余的部分,然后每次映射的坐标都分别加上0.5 倍的空余部分,即可中心化。
因为每次对数,都需要周围 4 \times 4个点,所以我对参考图像做了长度 1 的 padding。
优化
上面的代码有一个地方能优化,映射坐标处于同一个偏移[-1, 2] 内的点,只需要估计一场 f(x) ,不需要算每个坐标都估计一场 f(x) ,尤其是做放大运算,尺寸远远大于原尺寸的情况。
实现的话,需要维护一个当前的位置区间,超出区间就重新算 f(x) ,还在区间之内直接调用 f(x) 即可。