序言
控制点分析是研究进行分类问题的分析方式,是洞悉使用者偏爱和做使用者肖像的法宝之一。控制点分析的方式非常多,能认知经典之作又最基础的控制点方式 —— 层级控制点法(系统控制点) 的基本上基本上原理并将标识符用于实际的销售业务事例是本文的目标,与此同时这也会为认知先期与控制点相关的推文如 K-Means 等铺路。
责任编辑将详尽如是说如何 利用 Python 与此同时实现如前所述层级控制点的顾客分群,主要分为三个部份:
层级控制点详尽基本上原理如是说Python 代码两栖作战传授基本上原理部份
基本上原理如是说
难道它能被看做是两类的,因此或者它距近,或者它多多少少有共同的特点。领到统计数据集时,直接根据特点或分项来将样品进行分类的作法或者说更适宜销售业务能力较为强的人或有了不谋而合的分项如男女生各两类等限制性要求,因此责任编辑以样品间的距为控制点分项。为了能更快地精辟,他们调整了一下自学次序,将小部份解法尔后放,先从控制点结论的显示与分析侧发力。
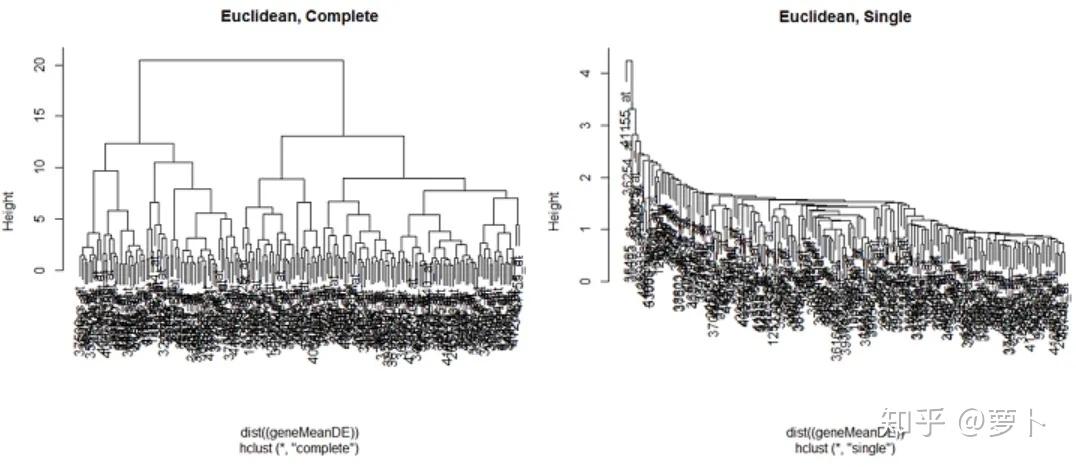
上面是有关层级控制点的几个示例。
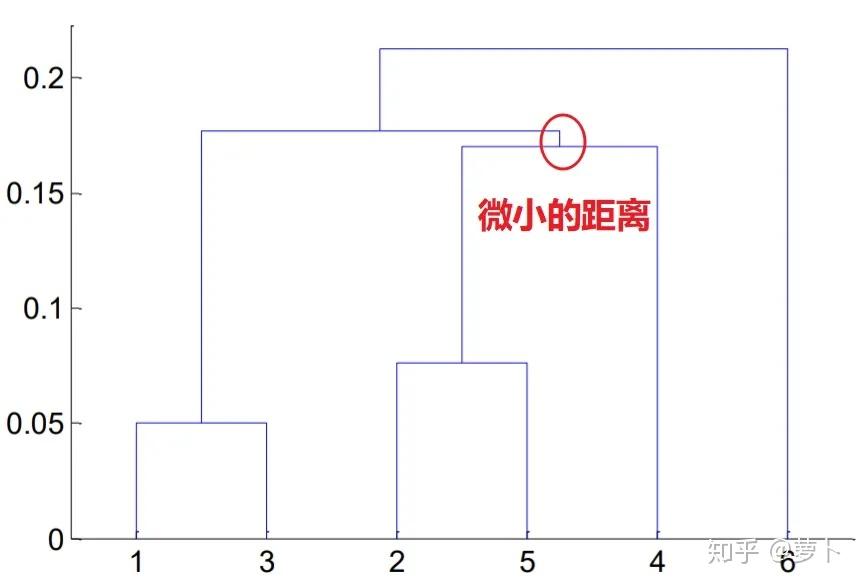
1、为什么都说层级Shahdol层级控制点法独一无二的控制点结论图?
因为Madurai的纵坐标会将每一个样品都范雄,并展现控制点的操作过程。十几个样品时候层级树就已经 “无法” 查阅了,况且成千上万的统计数据样品。
2、层级Shahdol怎么创建的?创建的基本上关键步骤?
或者说层级树的创建操作过程表示的就是控制点的操作过程,或者说透过层级树他们能窥见类间的层级关系(这两类与那两类相距假使),与此同时还能透过层级树决定最差的控制点特征值和窥见控制点方式(控制点次序的先后)
基本上关键步骤较为简约,只要短短 3 步:
排序每三个探测间的距将前段时间的三个探测圣皮耶尔县两类,将其看做一个整体排序与其他探测(类)间的距一直多次重复上述操作过程,直至所有的探测被圣皮耶尔县两类创建层级树的三个关键步骤虽然简约,但或者说也有令人迷惑的地方,因此为了让各位更快的从整体上去认知控制点操作过程而不是圄于细节,这里先直接放一个控制点操作过程图和对应的层级树
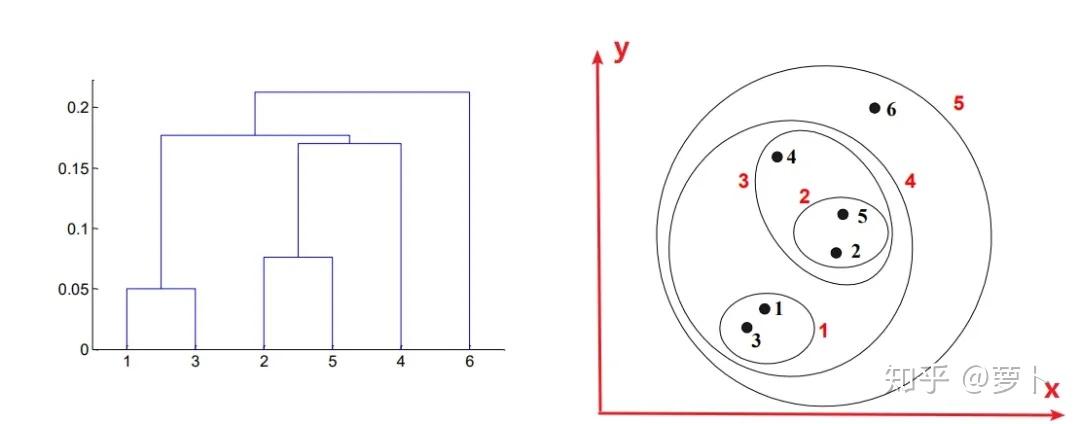
3、怎么从层级树中窥见控制点操作过程?
这一个简短的问题中或者说暗含不少门道,第一:**当三个点被分为两类时,是从纵坐标出发向上延伸,后形成一条横杠;当三个类被分为两类时,是横杠中点向上延伸。**这第一点中,横杠的数量就表示当所有的点都被圈为两类的时候经过了多少次控制点。
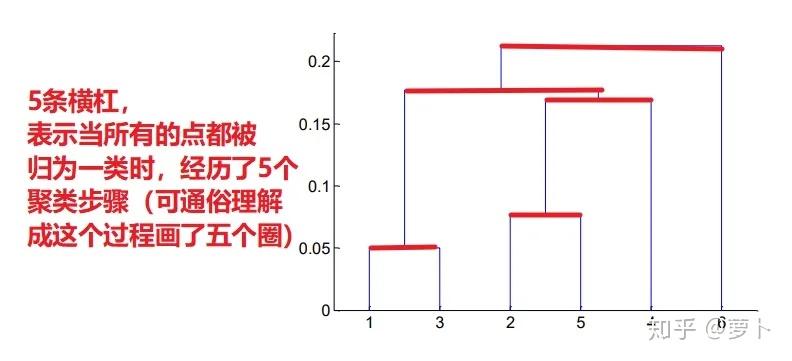
同样,横杠距纵坐标轴的高度也有玄机,毕竟每生成一个横杠就表示又有一次控制点了,因此他们能透过横杠的高度判断控制点的次序,结合上图右半部份的圆圈和数字标号也能窥见。
因此控制点次序便如下表:
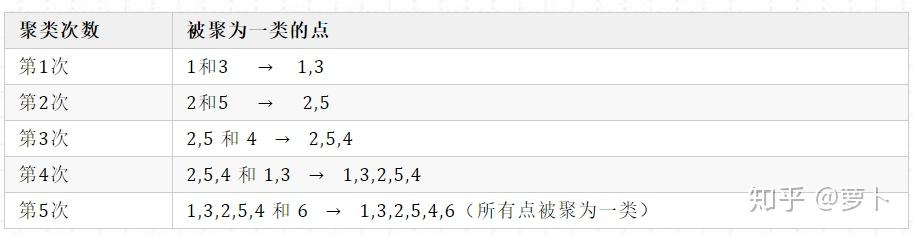
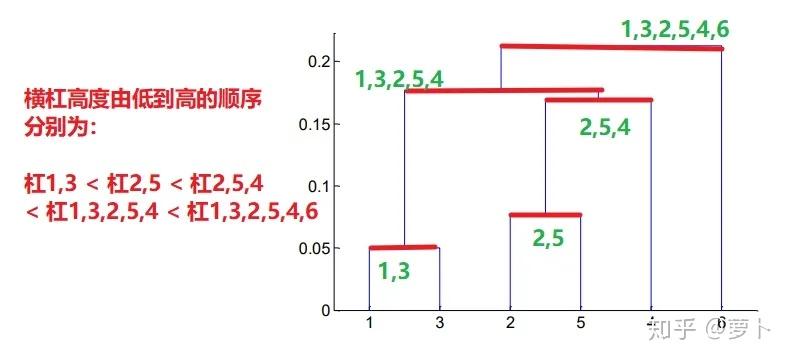
第二,整棵层级Shahdol由一棵棵小树组成,每棵小树代表了一个类,小树的高度即是三个点或三个类间的距,因此三个点间的距越近,这棵树就越矮小。
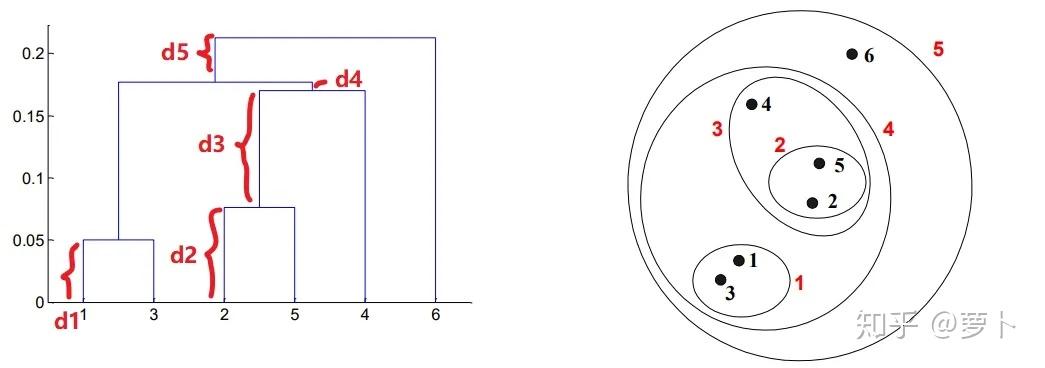
上面这一段仔细阅读的话对认知点与点,类与类,点与类间的距是如何在层级树上体现很有帮助。先从最矮的高度只有 d1 小树说起,这就是类 1,3 中三个孤立的点 1 和 3 间的距;同理,d2 为类2,5 中点 2 和 5 间的距。
而至于 d3, d4, d5 这三个距,他们并不像 d1 和 d2 那般表示的是一棵完整的树的高度,而更像是 “ 生长的枝干 ”,因为从第一点中的 “ 当三个类被分为两类时,是横杠中点向上延伸。” 能窥见 d3 是从类 2,5 横杠的中点往上延伸的,因此它表示会与另外的类聚成一起并形成一棵更大的树,图中即类 2,5 和点 4 被聚成一个新的类 2,5,4。
同理:
d4 表示类 2,5,4 与类 1,3 聚成新类 1,3,2,5,4d5 表示类 1,3,2,5,4 与点 6 聚成类 1,3,2,5,4,64、怎么从层级树中窥见控制点情况?能透过决定纵轴分界线可决定这些统计数据到底是分成多少类
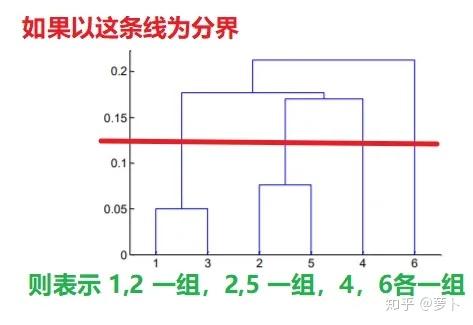
定好分界线后,只需要看距这条线横杠和单独的竖线即可,上图中距红线的横杠有两条(分别表示类1,2 和类2,5),单独的竖线也有两条,从纵坐标轴 4 和 6 上各延伸出的一条。同理可用到下图
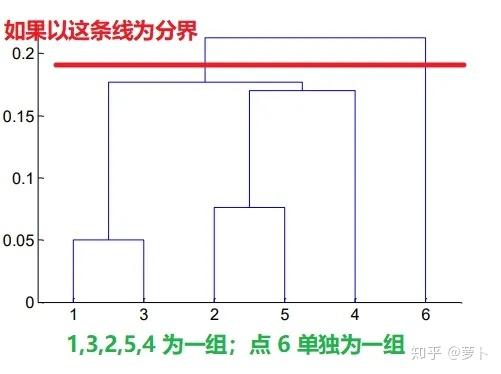
为什么最好不要分成 3 组:13,254,6 呢?
因为树的高度表示三个点间的距,因此 4 到 类25 的距只比到 类13 的距要多如下图所示的一点点,因此硬是把 4 跟 25 分成两类就有点牵强了,正因为这种牵强的进行分类方式可能会让他们忽略 4 这个点单独的价值,因此他们不如直接将 4 看做单独的两类。
推导与排序
接下来就是需要更加动脑的数学基本上原理和公式部份了,他们需要知晓点与点,类与类,点与类这三种距如何排序。
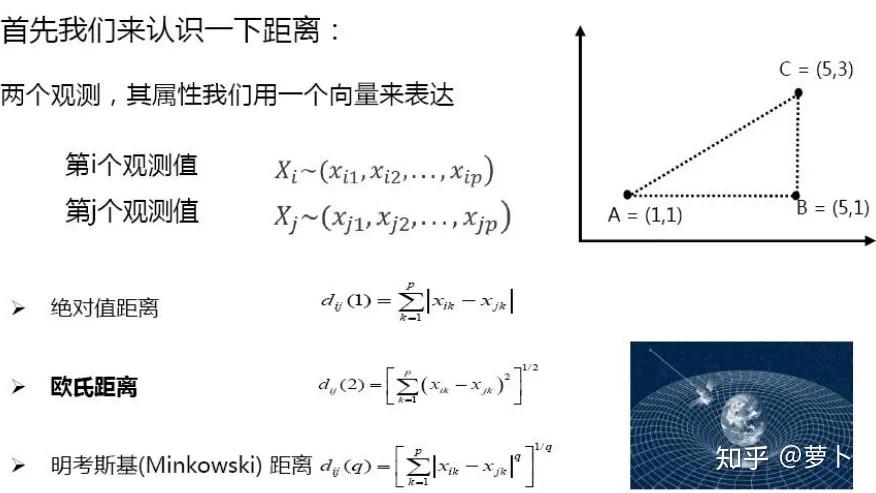
最包罗万象的是明考斯基距,因为 q 分别取 1 和 2 的时候就表示是绝对值距和欧氏距。点与点的距很好求,他们一般用的都是欧氏距,即初中自学的直角三角形三边关系,上图右上角点AC间的距(ab² + bc²) 后再开根号
而至于类与类间的距求法,或者说经过了一个演变,篇幅原因责任编辑只会一笔带过那些不常用的方式并将重心放在最常用和主流的方式上。
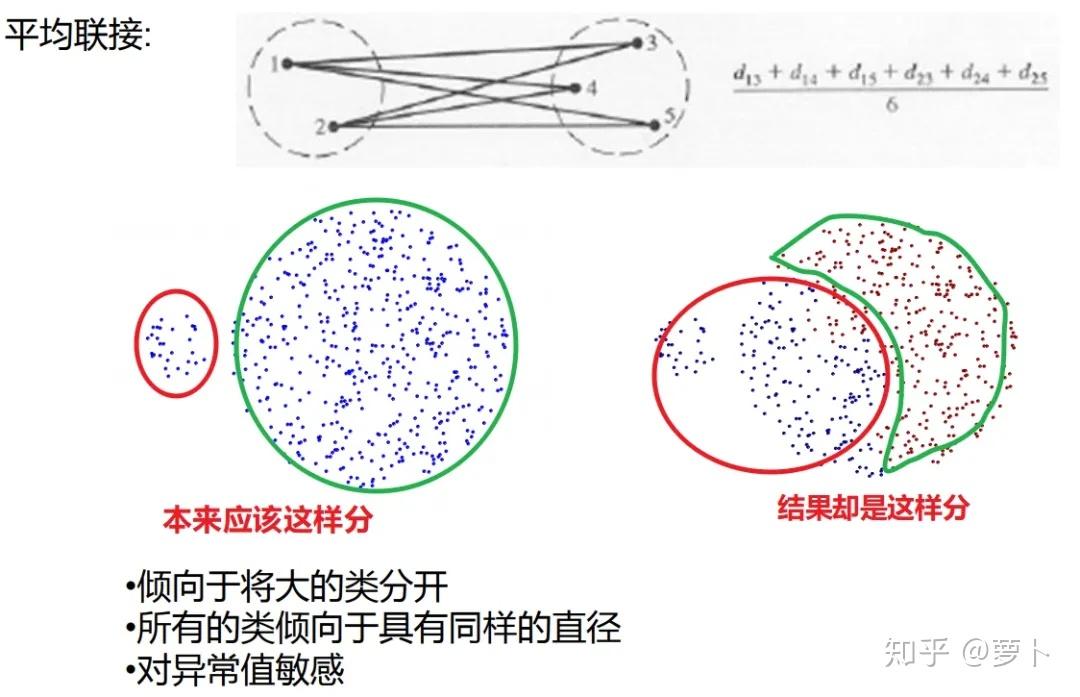
平均联接和重心法都已经较为少用了,现大多采用较少受异常值影响且不知统计数据分布的情况下依然能有较好表现的 Ward 法。
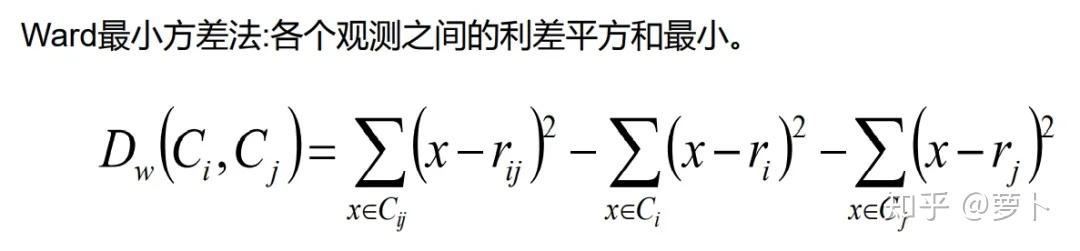
或者说 Ward 法的公式与方差分析相似,都是透过组间距来定夺点点/点类/类类间的距,Ward 法许多详尽的数学推导在网上有很多,这里他们直接展现最容易认知的一种:
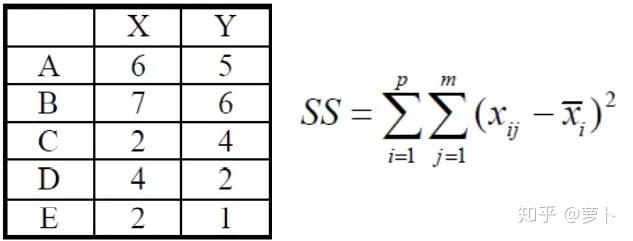
上图为已知的五个点和它 x,y 轴坐标,SS 为 Ward 最小方差法的公式。

当三个点被圣皮耶尔县两类时,这两类的组间差异 SS 便为其中一点的某一坐标与另外的所有坐标加加减减的一系列操作(通俗解释,或者说直接看上图的 SS 排序操作过程已经能认知。)
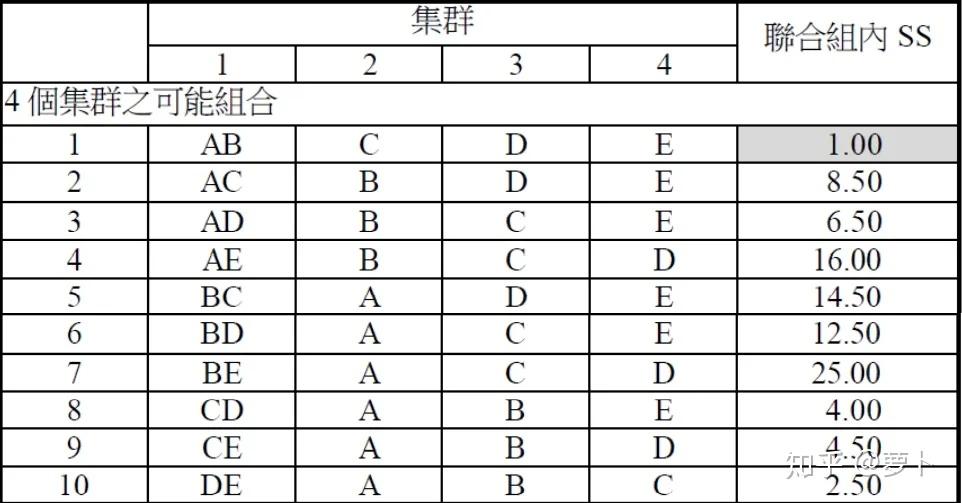
了解 Ward 最小方差法的基本上求解公式后,他们能从最简单的控制点形式开始:5个点聚成4类。这意味着其中三个点会被聚在一起,剩下三个点各自为两类,因此总共会出现 C52 = 10 种情况,每种情况的组内 SS 分别如下表:
同理,如果这 5 个点聚成 3/2/1 类的情况如下表:
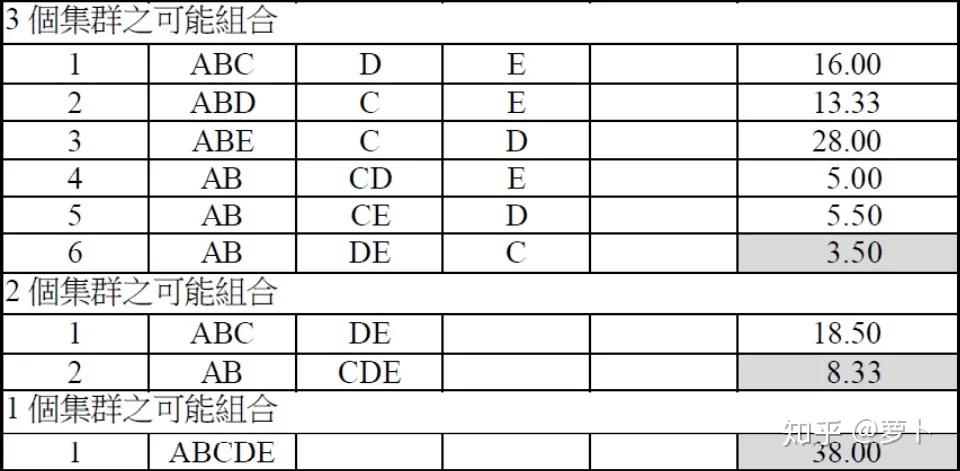
需要注意的是:聚成两类后排序出 AB 这三个的利方差最小后,在先期聚成3类,2类的时候就直接把A和B三个看做是同一个个体了,因此不会再出现A和B分开的局面。
结合三个表,他们便能得出如下结论:
如果需要被聚成 4 类,AB为两类,剩下3个点各为两类最好(SS 最小)如果需要被聚成 3 类,AB,DE为两类,剩下的 C 单独为两类最好如果需要被聚成 2 类,AB,CDE各为两类如果需要被聚成 1 类,对不起,我觉得没什么分析的必要在进入标识符两栖作战前,他们简单总结一下基本上原理部份提到的知识点:
层级树的阅读三个点间的距公式Ward 法求类内的组间差异,用以决定聚出的类别特征值标识符两栖作战
在正式两栖作战前,需要注意以下几点,首先原始统计数据通常需要经过处理才能用于分析:
缺失值异常值(极大或极小)进行分类变量需要转化为哑变量(0/1数值)进行分类变量类别不宜过多其次由于变量的量纲的不一样引起排序距的偏差,他们需要对统计数据进行标准化。与此同时不同的统计方式对统计数据有不同的要求:
决策树和随机森林允许缺失值和异常值聚类分析和回归模型则不支持缺失值1、控制点的时候,所有的 X 必须都是连续变量,为什么?
进行分类变量无法排序距,如某个变量表示的是性别,男和女;教育程度为小学,初中,高中,大学,那该变量在各个个体间的距怎么排序?因此做控制点分析时尽可能用进行分类变量。
2、那这些进行分类变量的价值难道就无法利用了吗?
能先根据其他的连续变量控制点,而后对分出来的类做描述性统计分析,这时候就能用上进行分类变量的价值了。另外一种方式是能在第一步就把进行分类变量也用上的控制点方式,不过需要结合实际销售业务。
以市场顾客调研为例,属于 “ 顾客的需求与态度 ” 这个分支,目的是依据调查问卷结论针对需求的统计数据分群,而调查分卷的问题中回答 “yes” 或者 “no” 类型的问题通常又会占一大部份,这时候我么能透过合并多个问题回答的结论来将多个进行分类变量组合,生成一个连续变量,以电信顾客的使用和需求情况为例:
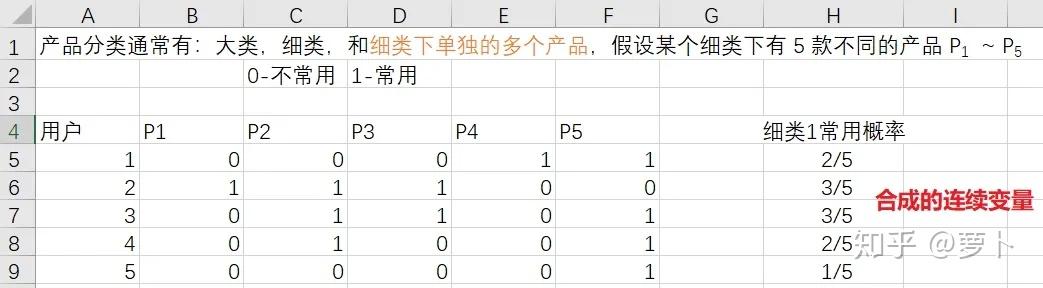
当然也还能排序进行分类变量间的 cos 相似度,即直接把进行分类变量设成距。总之,进行分类变量在控制点当中是一定需要处理的。
现在终于到了正式的标识符阶段,如果前面的基本上原理都认知好了,标识符的认知则可不费吹灰之力。这里他们使用一份公开的城市经济统计数据集,参数如下:
AREA:城市名称Gross:总体经济情况指数Avg:平均经济情况指数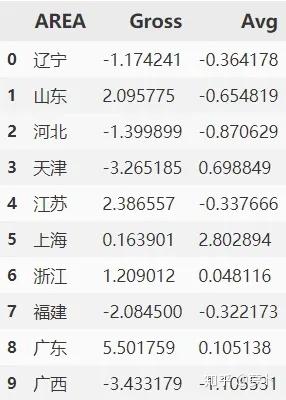
供。
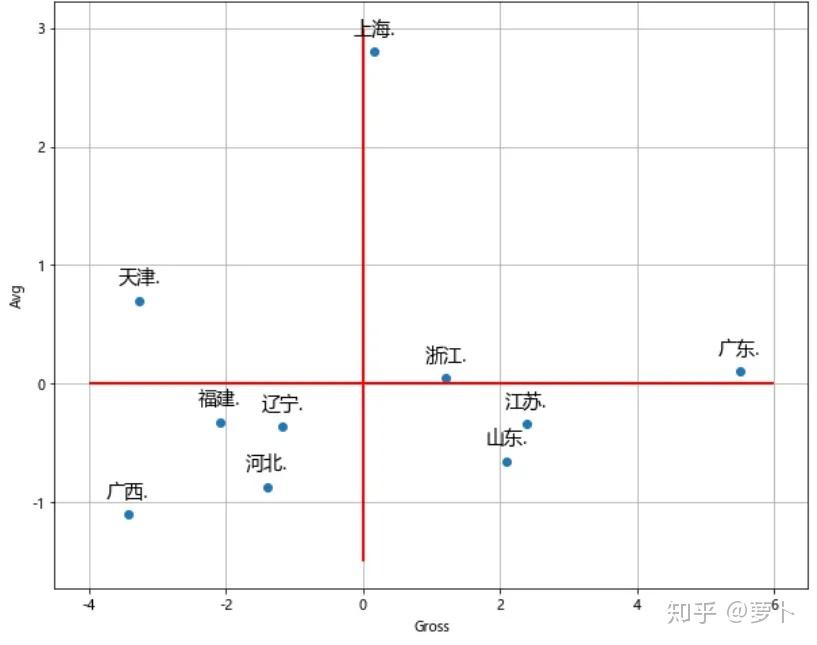
sklearn 里面没有层级控制点的函数,因此从 scipy 中导入
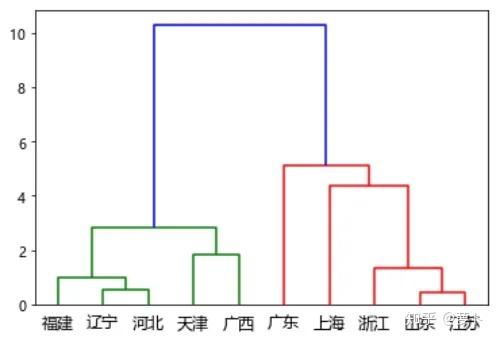
上面是层级控制点可视化:层级树
最后说一下,未来还会有 K-Means 等控制点方式的推文。作为精辟控制点方式的开端,他们只需知道层级控制点相比 K-Means 的好处是它不用事先指定他们需要聚成几类 (K-Means 算法标识符中的参数 k 指定)
这样一来,他们只需要把排序全权交给程序,最终能得出一个较为精准的结论。但缺点是随之而来的排序复杂度的增加。
因此层级控制点更适宜小样品;K-Means 更适宜大样品,在统计数据挖掘中也更常见,责任编辑分享就到这里,他们下期决策树见~
乎签名!











