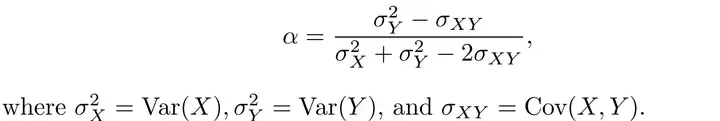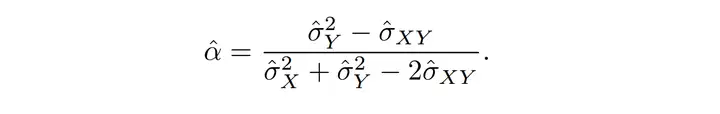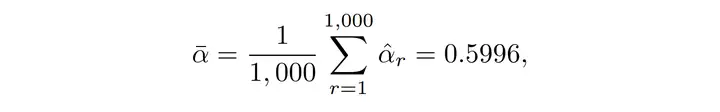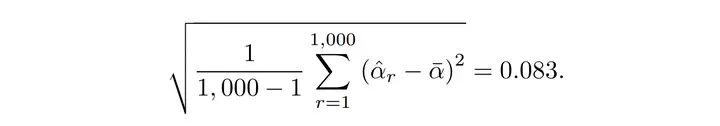Bootstrap概要
Bootstrap方式是非常管用的两类统计统计数据学上的估算方式,是史丹福统计统计数据系的副教授Bradley Efron(我曾碰巧去副教授服务部检举了一次)在归纳、概括宋人科研成果的基础上提出两类捷伊非模块统计统计数据方式。Bootstrap是两类非模块Monte Carlo方式,其本质是对探测重要信息展开再样品,从而对整体的分布优点展开统计统计数据推测。
因为该方式充分运用了取值的探测重要信息,不需要数学模型其他的假定和增加捷伊探测,因此具有Sitapur和成本低的特征。1980年代以来,随着电子计算机被导入到统计统计数据实践中来,此方式愈来愈畅销,在机器学习应用领域应用应用领域也很广为。
具体来说,Bootstrap通过重样品,能防止了Cross-Validation造成的样品减少难题,其二,Bootstrap也能用作缔造统计数据的乱数性。比如说,他们所津津乐道的乱数丛林演算法第二步就从原初体能训练统计数据集中,应用应用领域bootstrap方式有放回地乱数抽出k个捷伊自助式样品集,并继而构筑k棵进行分类重回树。
具体内容传授
上面他们用两个范例具体内容如是说bootstrap的基本原理和用语:
假定他们有三个金融资产X和Y,他们现在想资源整合这三个资产,使其资产女团的风险最轻。也就是找出两个α\alpha ,使Var(αX+(1−α)Y)Var(\alpha X+(1-\alpha)Y)最轻。这个难题数十年前罗兹索科夫斯基已经在其投资女团理论里得出了答疑,最优化的α\alpha抒发式如下:
但是现实生活中实际上他们并不知道σX2\sigma _X^2,σY2\sigma_Y^2以及σXY\sigma_{XY}的值,故而只能通过X和Y的一系列样品对其展开估算。并用估算值σX2^\hat{\sigma _X^2},σY2^\hat{\sigma_Y^2}以及σXY^\hat{\sigma_{XY}}代替σX2\sigma _X^2,σY2\sigma_Y^2以及σXY\sigma_{XY}插入公式:所以他们唯一的任务就是合理地估算σX2^\hat{\sigma _X^2},σY2^\hat{\sigma_Y^2}以及σXY^\hat{\sigma_{XY}},传统方式中他们一般会考虑直接使用样品方差(sample variance)去估算σX2\sigma _X^2,σY2\sigma_Y^2以及σXY\sigma_{XY}的值,然而自从有了Bootstrap之后,他们有了另两类方式与途径,能更好地去做估算整体的分布优点,即不仅能估算α\alpha ,还能估算α\alpha 的方差、中位数等值。上面就讲讲Bootstrap究竟是如何做到这一点的:Bootstrap步骤:
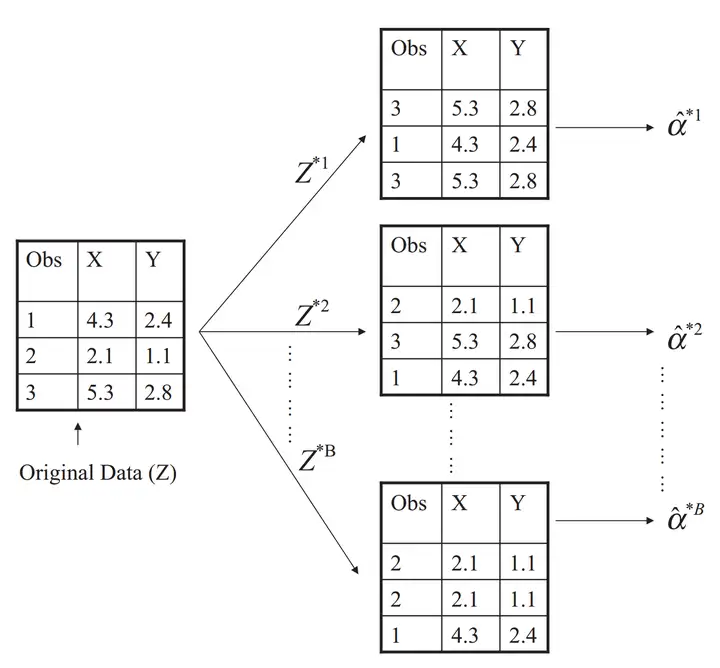
1. 在原有的样品中通过重样品抽出一定数量(比如说100)的新样品,重样品(Re-sample)的意思就是有放回的抽出,即两个统计数据有能被重复抽出超过一次。
2. 基于产生的新样品,计算他们需要估算的统计统计数据量。
在这范例中,他们需要估算的统计统计数据量是α\alpha ,那么他们就需要基于新样品的计算样品方差、协方差的值作为σX2^\hat{\sigma _X^2},σY2^\hat{\sigma_Y^2}以及σXY^\hat{\sigma_{XY}},然后通过上面公式算出两个α^\hat{\alpha}
3. 重复上述步骤n次(一般是n>1000次)。
在这个范例中,通过n次(假定n=1000),他们就能得到1000个αi\alpha_i。也就是α1,α2,⋯,α1000\alpha_1,\alpha_2,\cdots,\alpha_{1000}。
4. 最后,他们能计算被估算量的均值和方差(不用关注最后的具体内容数值,这与原本的样品有关):
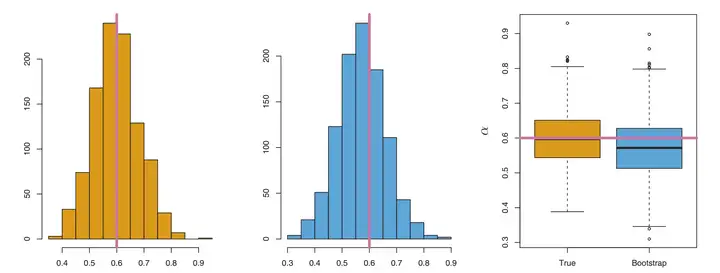
他们发现,通过Bootstrap方式他们竟然不仅能估算α\alpha的值( 这点普通方式也能很容易做到),还能估算α\alpha的accuracy也就是其Standard Error。这可是只利用原有的样品展开一次估算所做不到的。那么Bootstrap对于分布优点的估算效果究竟如何呢?请看下图:左边是真实的α\alpha 分别,右边则是基于bootstrap方式得到的1000个α\alpha 的分布,能看到,二者是比较相近的,也就是说Bootstrap有着不错的估算效果。而且当重复次数增多,Bootstrap的估算效果会更好。不仅是α\alpha 的标准差,如果他们想估算α\alpha 的中位数、分位数等统计统计数据量,也是能通过Boostrap方式做到的,其整个流程能用上面一张图诠释:
本质上,Bootstrap方式,是将一次的估算过程,重复上千次上万次,从而便得到了得到上千个甚至上万个的估算值,于是利用这不止两个的估算值,他们就能估算
α\alpha均值以外的其他统计统计数据量:比如说标准差、中位数等。
Statistical Learning with Applications in R》
说在后面
关于机器学习的内容还未结束,请持续关注该专栏的后续文章。
更多内容请关注我的专栏:R Language and Data Mining
或者关注我的知乎账号:温如